참고: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 5 - Current Mirrors and Biasing Techniques (pg. 134~146)
5. Current Mirrors and Biasing Techniques
5.1. Basic Current Mirrors
Introduction to Current Sources

Fig. 5.1은 current source의 application을 나타냅니다.
Fig. 5.1(a)에서는 current source I1이 PMOS에 bias voltage를 가하는 방식으로 구현되었습니다.
Fig. 5.1(b)에서는 tail current source Iss가 NMOS로 구현되었습니다.
Current source의 output resistance와 capacitance, voltage headroom과 output current magnitude 간에 tradeoff가 있습니다.
또한 current source는 supply, process, temperature dependence의 이슈가 있습니다.
Output noise current와, 다른 current source와 matching하는 문제도 있는데, 이는 각각 Ch7: Noise, Ch14: Nonlinearity and Mismatch에서 알아본다고 합니다.
Drawbacks of a Resistive Divider


Fig. 5.2는 MOSFET이 안정적인 current source로 작동하기 위한 방법 중 하나인 resistive divider를 소개합니다.
M1이 saturation에 있다고 가정하면, Iout은 (5.1)과 같이 나타납니다.
M1의 Vgs = R2/(R1+R2)이기 때문입니다.
그런데 이 resistive divider의 문제점은, Iout이 PVT variation의 영향을 많이 받는다는 것입니다.
(PVT variation에 대한 설명은 아래 링크 참고)
PVT(Process, Voltage, Temperature) Variation
출처:https://www.physicaldesign4u.com/2020/07/pvt-process-voltage-temperature.html PVT (Process, Voltage, Temperature)VLSI PHYSICAL DESIGN FOR FRESHER will be helpful for the Physical design engineer and to find physical design engineer jobs.www.physica
soobdal.tistory.com
(5.1)의 Iout 식에 있는 Vth는 wafer별로 50~100mV씩 차이가 날 수 있고, μn과 Vth 모두 온도의 영향을 받습니다.
따라서 resistive divider로 구현한 current source는 Iout이 안정적이지 않다는 문제가 있습니다.
그래서 더 안정적인 current source를 만들 수 있는 다른 방법이 필요합니다.
(특히, headroom을 덜 소모하고 drain에서 voltage swing을 더 크게 가져가기 위해 Vov를 작게 설정하면, Iout이 PVT variation에 의한 영향을 더 많이 받게 됩니다.)
Reference Generator

안정적인 current source를 위해 사용할 구조는 reference로부터 전류를 복사해 오는 겁니다.
Reference current, Iref를 정확하게 생성하는 안정적인 current source는 이미 있다고 가정합니다.
Fig. 5.3과 같이, 안정적인 Iref를 I1과 I2에 복사하여 사용하는 것입니다.
(이 단원에서는 복사하는 방법만 배우고, reference generator에 대해서는 Ch12: Bandgap Reference에서 배울 것입니다.)
Current Mirror
그렇다면 reference current를 어떻게 복사할 수 있을까요?
Fig. 5.4에서 Iref를 복사한 전류인 Iout이 Iref과 같다는 것을 어떻게 알 수 있을까요?

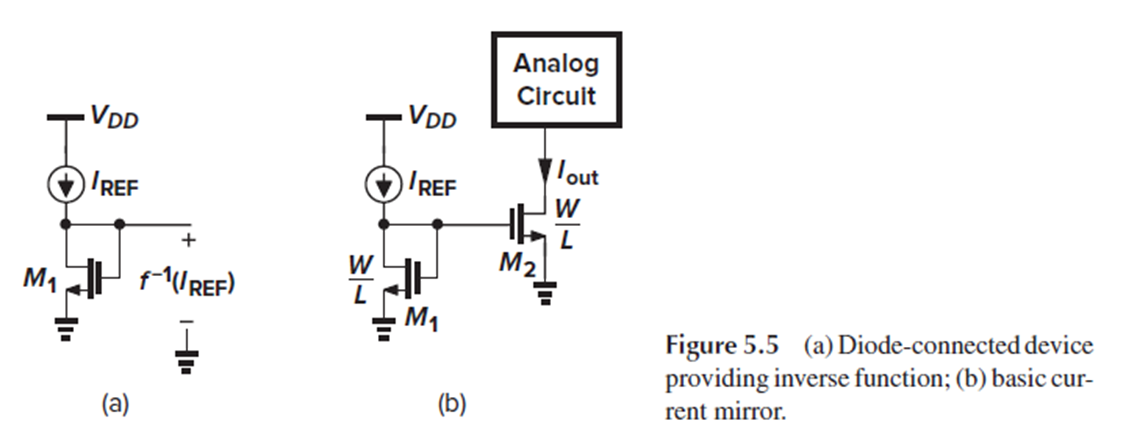
Channel-length modulation이 없고, MOSFET이 saturation에 있다면 MOSFET의 drain current는 Vgs의 함수입니다.
따라서 Fig. 5.5(b)의 회로에서, M1에 Iref가 흐르도록 하는 Vgs를 M2에 똑같이 인가하면, M2에도 Iref가 흐르게 됩니다.
Fig. 5.5(b)의 구조를 ‘current mirror’라고 합니다.
M1과 M2의 크기는 같을 필요가 없습니다.
Channel-length modulation을 무시하면, Iref와 Iout을 (5.2), (5.3)으로 나타낼 수 있어, Iref와 Iout 간에 (5.4)의 관계가 도출됩니다.
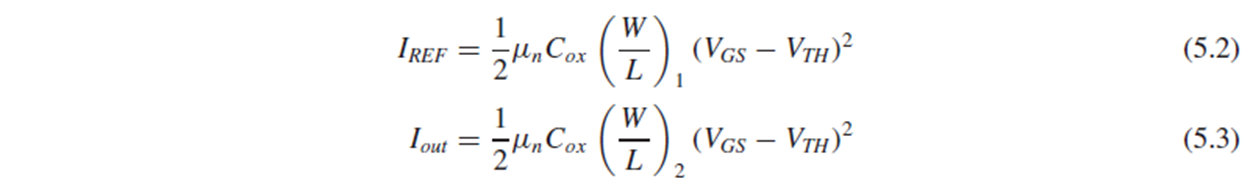
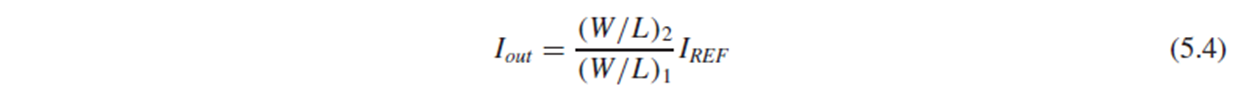
따라서 M1과 M2의 W/L 값을 조절하여 Iout의 값을 설정할 수 있게 됩니다.
Diode Connection in Current Mirror
여기서 Iref를 생성하는 MOSFET은 꼭 Fig. 5.5(b)에서처럼 diode여야 합니다.
먄약 Fig. 5.6에서처럼 M1이 diode가 아니고, 별도의 Vb가 M1과 M2의 gate에 인가되고 있다면, 그 회로는 current mirror가 될 수 없습니다.
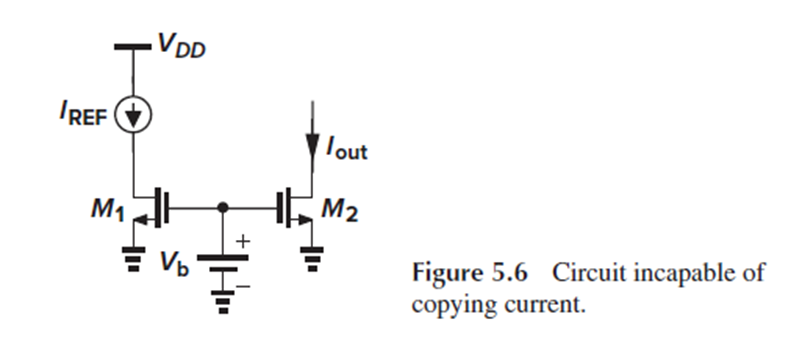
Diode connection이 current mirror에서 중요한 이유는 다음과 같습니다.
Fig. 5.5(b)에서 diode-connected인 M1은 drain과 gate가 연결되어 있어서, Vds = Vgs이므로 saturation 조건인 Vds > Vgs-Vth를 항상 만족합니다(Vgs > Vth이기만 하면).
그러면 M1에 흐르는 Iref(원인)에 의해 Vgs(결과)가 설정되고, 같은 Vgs(원인)가 M2에도 인가되어 M2에도 Iref에 비례하는 전류(결과)가 흐르도록 하는 것이 current mirror의 원리입니다.
그런데 diode 연결이 없는 Fig. 5.6에서는 Iref에 의해 M1과 M2의 Vgs가 설정되는 것이 아니라, 반대로 Vb(원인)에 의해 Iref(결과)와 Iout(결과)이 설정되게 됩니다.
Fig. 5.6은 원인과 결과가 뒤바뀐 경우로, 전류 ‘복사'라고 할 수 없겠죠. 따라서 current mirror가 될 수 없습니다.
Current Mirror Chain
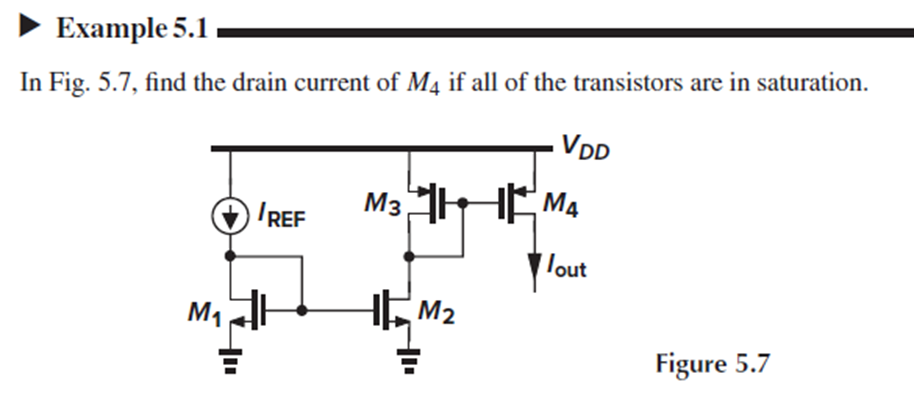
Fig. 5.7의 current mirror 구조에서, 모든 트랜지스터가 saturation에 있을 때 M4의 drain current를 구하는 문제입니다.
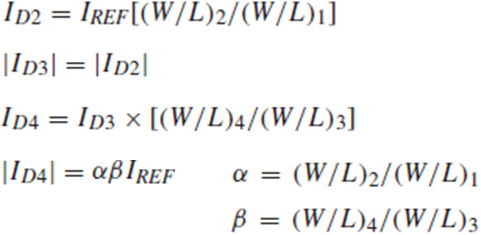
우선 Iref를 가장 먼저 복사하는 M2의 drain current는 Iref*[(W/L)2/(W/L)1]입니다.
M4는 M3의 drain current를 복사하는데, M3과 M2에 흐르는 전류가 같으므로 M4에는 Iout = Iref*[(W/L)4/(W/L)3]*[(W/L)2/(W/L)1]이 흐릅니다.
[(W/L)4/(W/L)3]*과 [(W/L)2/(W/L)1]에 따라 Iout을 조절할 수 있습니다.
이 example에서 봤듯이, Iout은 Iref에 W/L 비율을 여러 개 곱한 형태입니다.
Current mirror가 여러 단 달려서 W/L의 오차가 누적되면 원하는 Iout을 만들 수 없겠죠.
따라서 current mirror chain이 너무 길어지지 않도록 해서 원하는 값과의 오차를 줄여야 합니다.
Typical Application of Current Mirror
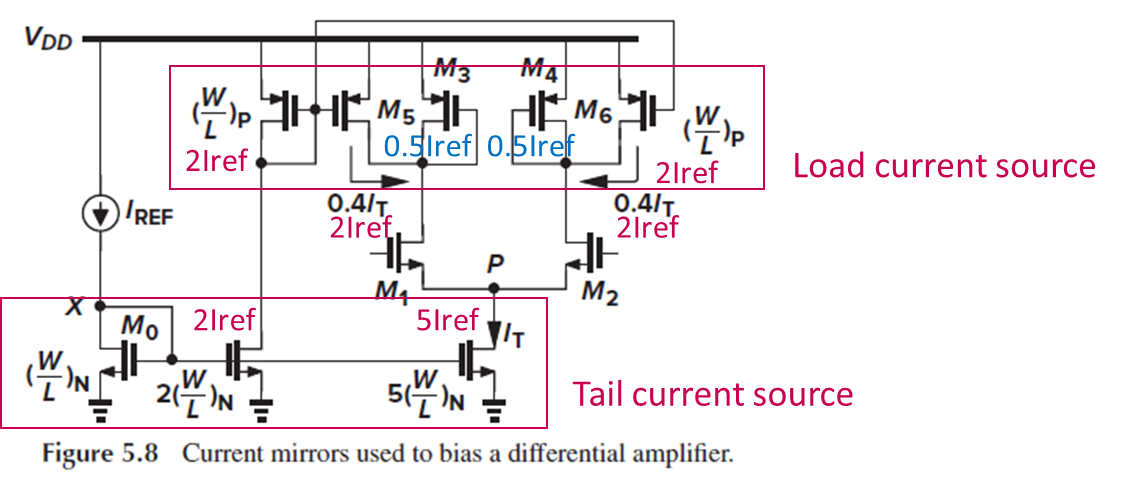
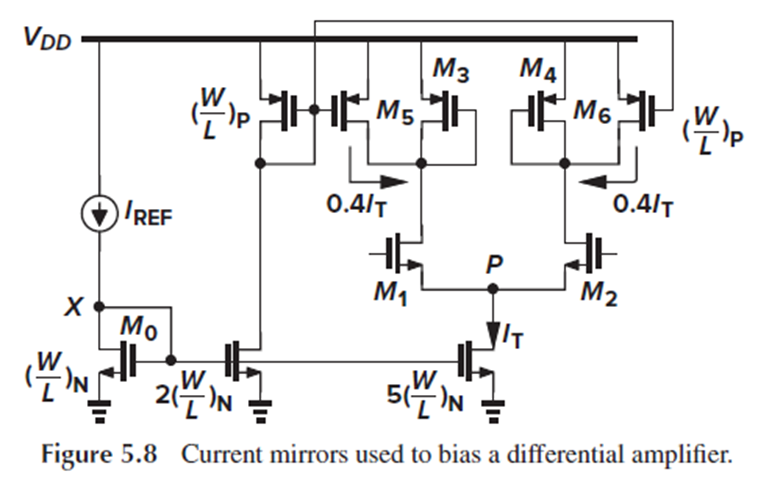
Fig. 5.8는 current mirror의 typical한 application을 나타냅니다.
Fig. 5.8에서 current source는 differential pair의 tail current source로도 쓰였고, load current source를 위한 PMOS mirror로도 쓰였습니다.
PMOS mirror가 없었다면 M3와 M4에 각각 drain current가 2.5Iref씩 흘렀을 텐데, PMOS mirror로 인해 0.5Iref로 줄었습니다.
이렇게 M3와 M4의 drain current가 감소하면서, differential amp의 gain이 증가하는 효과가 있습니다.
Sizing Issues
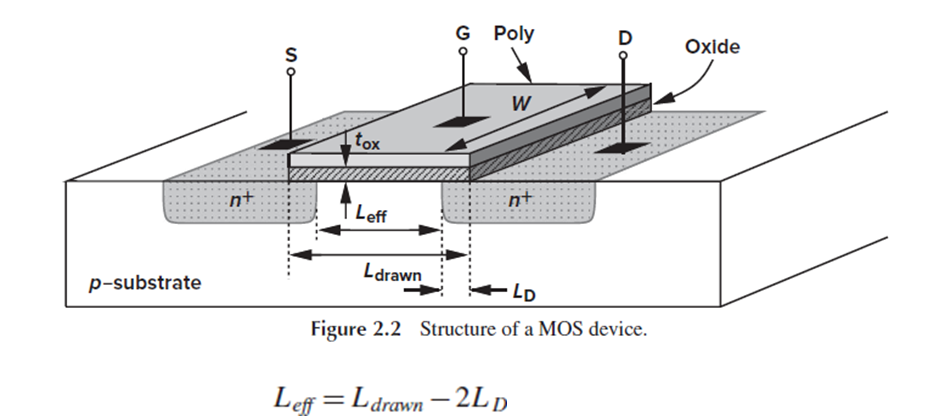
Current mirror에서는 주로 트랜지스터의 L을 고정시키고, W를 바꿔 W/L값을 변화시킵니다.
L을 고정시키는 이유는, source와 drain 영역의 side-diffusion(Ld)으로 인한 오차를 최소화하기 위해서입니다.
Ch2 내용을 복습하자면, 우리가 통상 말하는 L은 Leff이고, 설계자가 레이아웃 상에서 지정할 수 있는 길이는 Ldrawn입니다.
Leff는 Ldrawn에서, n+를 doping할 때 생기는 side diffusion에 의해 줄어든 길이 2Ld를 뺀 길이입니다.
설계자가 Ldrawn을 조절한다고 해도, Ld는 맘대로 조절할 수 없기 때문에, Leff를 원하는 값으로 맞추기 어렵습니다.
예를 들어, Ldrawn을 2배로 설정해도, Leff가 2배 되지는 않는다는 것이죠.
또한, short-channel device에서는 L에 따라 Vth가 달라지기도 합니다.
따라서 W/L 비율은 W값만 바꿔 조절하는 게 낫습니다.
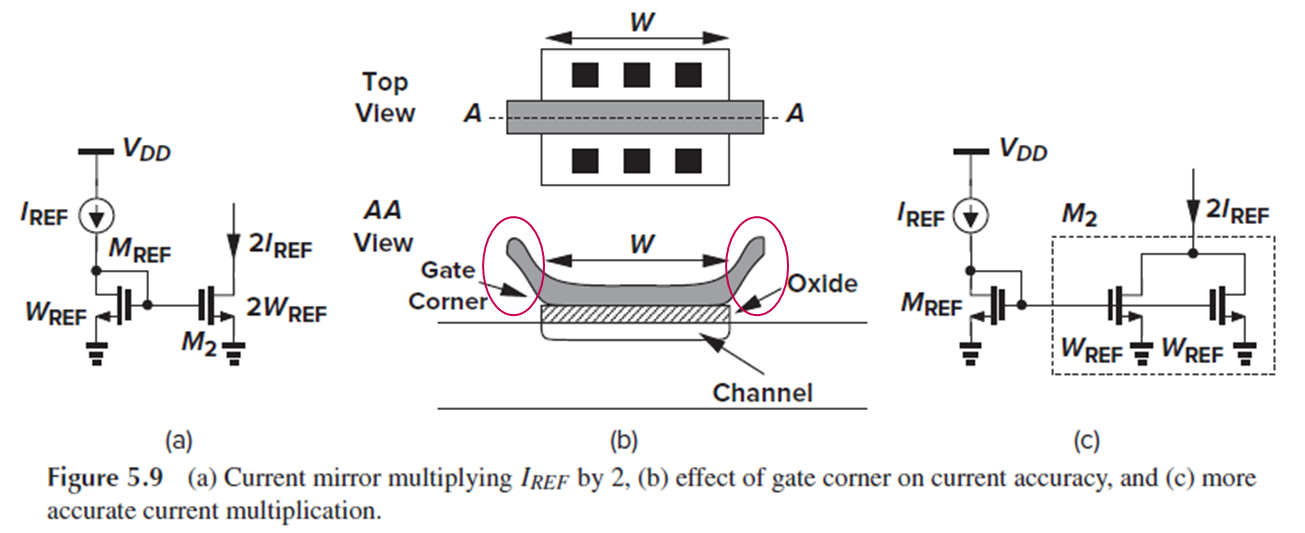
Iref로부터 2Iref를 생성하고 싶다고 가정해 봅시다. (Fig. 5.9(a))
앞선 논의에 의하면 M2의 W를 Wref의 2배로 설정하면 되겠죠?
그런데 실은, W도 정확한 scaling이 어렵다고 합니다.
MOSFET의 gate는 원래 직사각형으로 설계되지만, 공정에서 모서리 부분이 이상적으로 형성되지 않기 때문입니다.
따라서 설계자가 지정한 Wdrawn과 실제로 형성되는 gate의 폭 W가 일치하지 않게 됩니다.
즉, W를 두 배로 늘려서 MOSFET을 설계하더라도, 모서리 부분 때문에 전류가 정확히 두 배로 흐르지 않을 수 있습니다.
그래서, W/L을 조정하는 대신, “unit” transistor를 직렬 혹은 병렬로 연결하는 방법을 사용합니다. (Fig. 5.9(c))
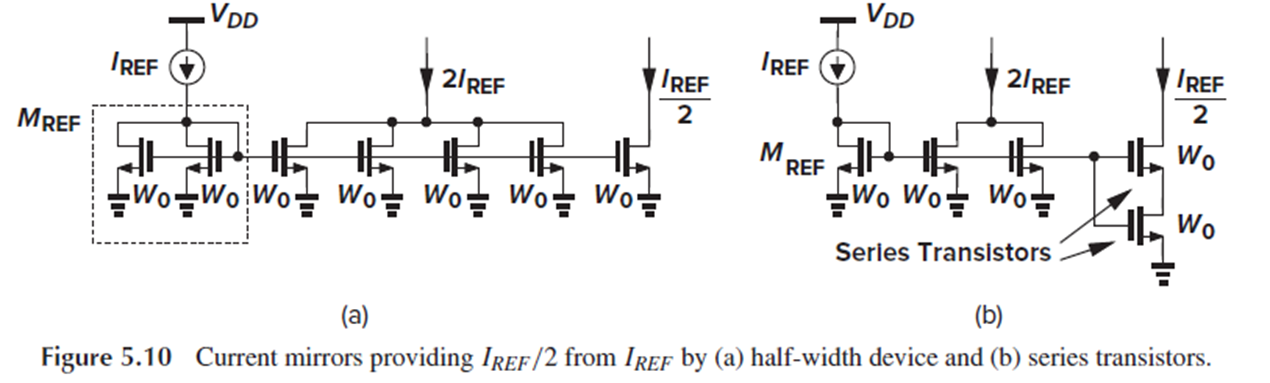
Fig. 5.10(a)에서 Mref는 W=W0인 unit transistor 2개로 이루어져 있고, drain current로 Iref가 흐르고 있습니다.
Unit transistor를 4개 써서 W를 Mref의 2배로 만들면, 그 부분에는 2Iref가 흐를 것입니다.
Unit transistor를 1개 써서 W를 Mref의 ½배로 만들면, 그 부분에는 1/2Iref가 흐르겠죠.
(Fig. 5.10(b)) Unit transistor를 직렬로 연결해서도 1/2Iref를 만들 수 있습니다.
Unit transistor 2개를 직렬로 연결하면 L을 2배 증가시키는 효과라서, W/L를 ½배로 만들 수 있습니다.
이렇게 unit transistor를 직렬로 연결하면, transistor 하나의 L값을 증가시킬 때와는 달리 Ld로 인한 오차 없이 equivalent한 L값을 늘릴 수 있습니다.
즉, 2Leff = 2(Ldrawn-2Ld) 효과를 얻을 수 있습니다.
* 여기서 직렬로 연결된 unit transistor는 cascode가 아닙니다.
이 구조에서는 상단 transistor의 voltage drop으로 인해 하단 transistor의 Vds가 낮을 확률이 높아, 하단 transistor가 triode region에 있을 확률이 높습니다.
상단, 하단 transistor가 모두 saturation에 있어야 cascode이므로, 이 구조는 cascode가 아닙니다.
Cascode Current Mirrors
지금까지의 논의에서는 channel-length modulation을 무시했습니다.
그런데 실제로는 channel-length modulation이 current mirror의 전류 복사에 엄청난 영향을 미칩니다.
특히 current source의 W를 줄여 output capacitance를 줄이기 위해서, L를 줄일 때 이 영향이 커집니다.
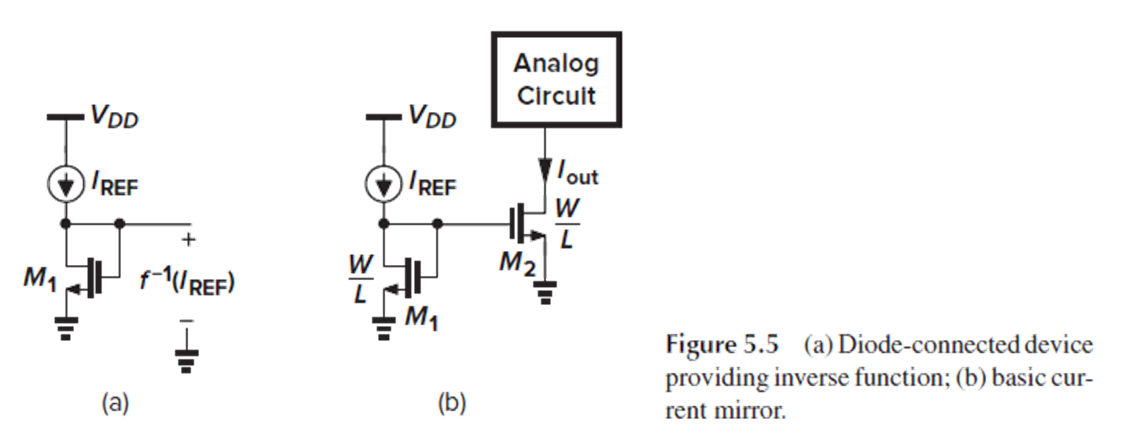
Channel-length modulation을 고려하면 Fig. 5.5(b)의 current mirror에서 Id1과 Id2는 각각 (5.5), (5.6)과 같습니다.
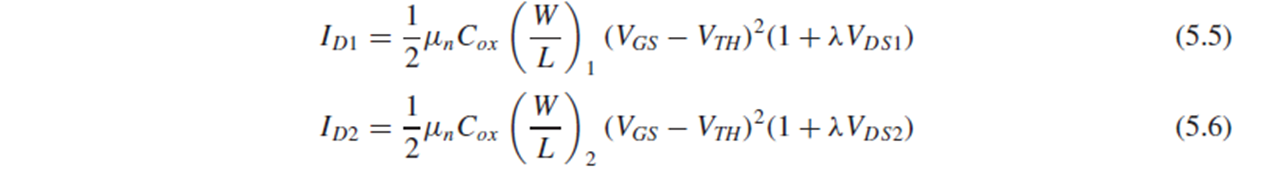
Id2와 Id1의 비율도 (5.7)처럼 λVds 항을 포함한 식이 됩니다.
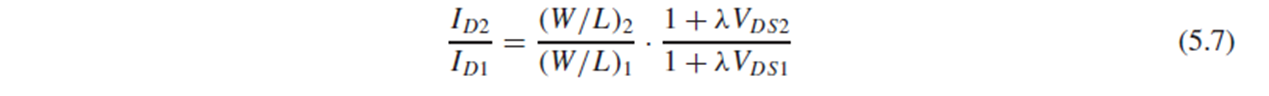
(5.7)에서 Vds1=Vds2이면 channel-length modulation으로 인한 항을 없앨 수 있겠지만, Vds1=Vds2는 항상 성립하는 것이 아니죠.
Current mirror에서 diode 구조에 의해 Vds1=Vgs1이고, M1과 M2의 gate가 연결돼 있으니까 Vgs1=Vgs2라 Vds1=Vgs1=Vgs2까지는 항상 성립합니다.
그렇지만 Vgs2=Vds2가 아니라서 Vds1=Vds2가 성립하지 않고, 따라서 channel-length modulation의 영향이 (5.7)에 살아 있게 됩니다.
우리는 current mirror에서 channel-length modulation에 의한 오차를 없애기 위해서 Vds1=Vds2를 만들고 싶습니다.
그 방법으로 두 가지가 소개되는데, (1) Vds2 값을 Vds1 값에 맞추기, (2) Vds1 값을 Vds2 값에 맞추기입니다.
First Approach: Make Vds2 equal to Vds1
첫 번째로, Vds2 값을 Vds1에 맞추는 방법입니다.
Ch3에서 cascode device는 current source를 “shield”해서, current source 양단의 voltage 변화를 줄일 수 있다고 했습니다.
Fig. 5.12(a)에서, Vp가 변하더라도 Vy는 비교적 일정하게 유지될 수 있는 것입니다.
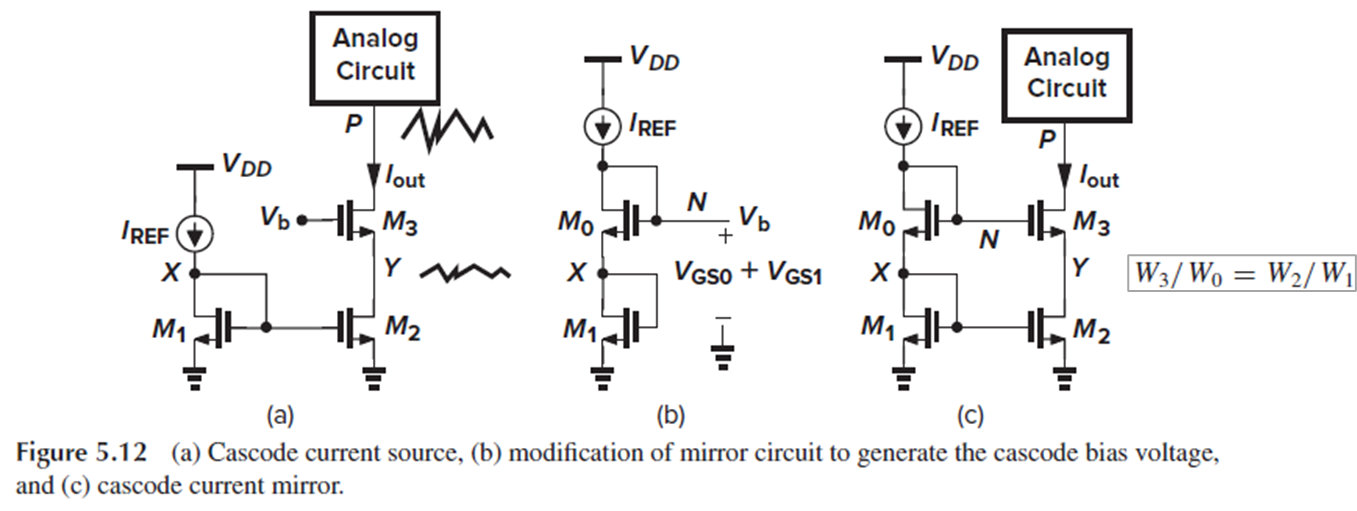
여기서 Vds2=Vds1임을 보장하기 위해서는, Vb를 알맞게 설정해야 합니다.
(Vds2=) Vb-Vgs3 = Vds1 (=Vgs1), 즉 Vb = Vgs3+Vgs1이도록 Vb를 설정해야 합니다.
우리는 왼쪽 branch를 활용해서 Vb를 Vgs3+Vgs1으로 설정하고 싶습니다.
만약 Fig. 5.12(b)처럼 M1 위에 diode인 M0를 쌓으면, M0의 gate 전압은 Vgs0+Vds1 = Vgs0+Vgs1이 됩니다.
그럼 Vgs0 = Vgs3이기만 하면, M0의 gate 전압이 Vgs0+Vgs1 = Vgs3+Vgs1이 되어, 우리가 원하는 Vb값이 됩니다. (Fig. 5.12(c))
Vgs0 = Vgs3을 위해서는 M0와 M3의 L은 같게 설정하고, W3/W0 = W2/W1이도록 해야 합니다.
M1 → M2, M0 → M3로 전류가 복사되는 비율이 같아야 M3, M2에 같은 크기의 전류가 흐르기 때문입니다.
Fig. 5.12(c)의 current mirror에서는 body effect가 있더라도 전류 복사가 정확하게 일어날 수 있습니다.
M1과 M2의 source는 gnd에 연결돼 있어 Vsb=0(기본적으로 Vb=0)라 body effect가 나타나지 않지만, M0와 M3의 source는 gnd에 연결돼 있지 않기 때문에 body effect가 나타납니다.
그런데 Vds2=Vds1이므로 M0와 M3의 Vs가 같기 때문에, body effect term 값이 같게 나타납니다.
따라서 (5.7)의 전류 복사 비율식의 분자, 분모에서 body effect term이 서로 상쇄되어, 전류 복사가 정확하게 일어날 수 있는 것입니다.
- Drawback of First Approach
이 방법은 높은 output impedance와 정확한 Iout을 얻을 수 있다는 장점이 있긴 하지만, voltage headroom을 많이 잡아먹는다는 단점이 있습니다.
편의를 위해 Fig. 5.12(c)에서 body effect를 무시하고 모든 transistor가 동일하다고 생각해 봅시다.
그러면, node P에서 가능한 최소 전압은 (Vgs3-Vth3)+Vds2 = (Vgs0-Vth)+Vgs1으로, 결과는 (5.12), (5.13)과 같습니다.
(모든 transistor가 saturation에 있어야 하므로 Vds3 > Vgs3-Vth3 적용)
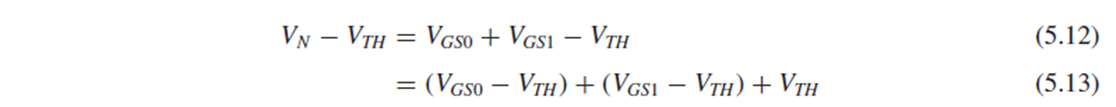
즉, node P에서 가능한 최소 전압은 overdrive voltage 2개와 threshold voltage 1개를 더한 값입니다.
이 값은 이어서 살펴볼 회로의 voltage headroom에 비해 큰 값입니다.
- Build-up for Second Approach
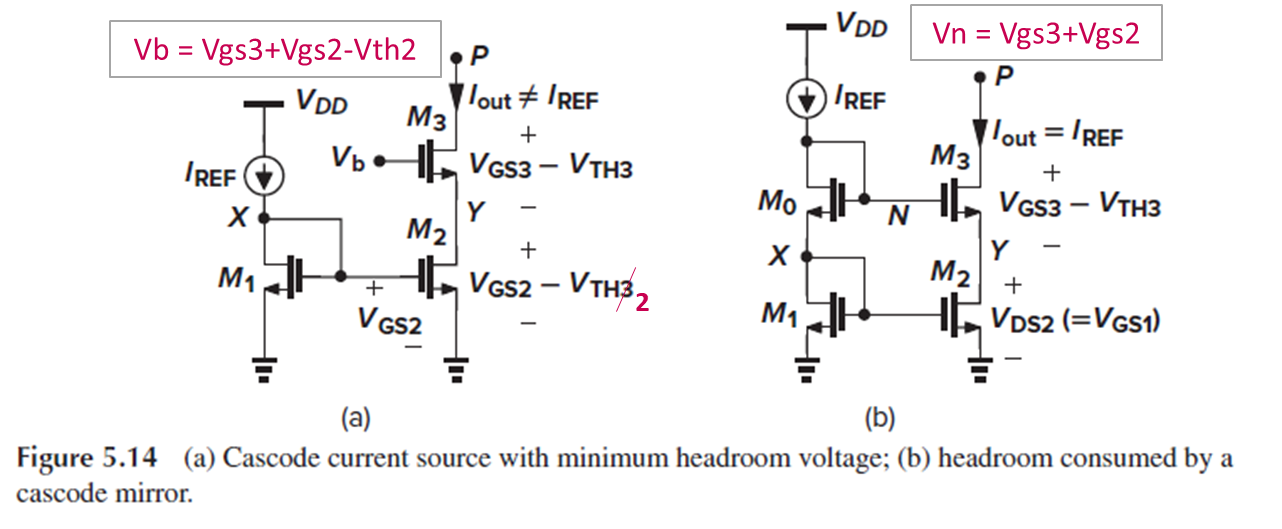
Fig. 5.14(a)를 보면, Vb는 Vgs3+Vgs2-Vth2까지 낮아질 수 있습니다.
그때 가능한 Vp의 최소값은 overdrive voltage 2개의 합이 됩니다.
Fig. 5.12(c)(=Fig. 5.14(b))의 회로에서는 Vb = Vgs3+Vgs2이었고, Vp의 최소값은 overdrive voltage 2개의 합에 Vth를 더한 값이었습니다.
Fig. 5.14(a)의 경우에는 Vb = Vgs3+Vgs2-Vth2로 설정함으로써 Vth만큼의 voltage headroom을 더 확보한 셈이죠.
그런데 Fig. 5.14(a) 회로는 voltage headroom을 확보할 수는 있지만, M1과 M2의 Vds가 같다는 보장이 없어, Iout이 Iref를 정확하게 복사하지 못하는 단점이 있습니다.
Fig. 5.14(b) 회로는 voltage headroom이 Vth만큼 작은 대신, 전류를 더 정확하게 복사할 수 있습니다.
Second Approach: Make Vds1 equal to Vds2
아까는 Vds2를 Vds1와 같게 맞춰서 channel-length modulation을 없애는 방법을 알아봤고, 이제는 Vds1를 Vds2와 같게 맞추는 방법을 알아보겠습니다.
Iref를 생성하는 왼쪽 branch를 변형하겠다는 것입니다.
(이 방법은 first approach에서 소개된 두 방법의 장점만을 취하는 방법이기도 합니다.
Voltage headroom에서 Vth를 깎지 않으면서, 전류 복사도 정확하게 할 수 있는 방법이라는 거죠.)
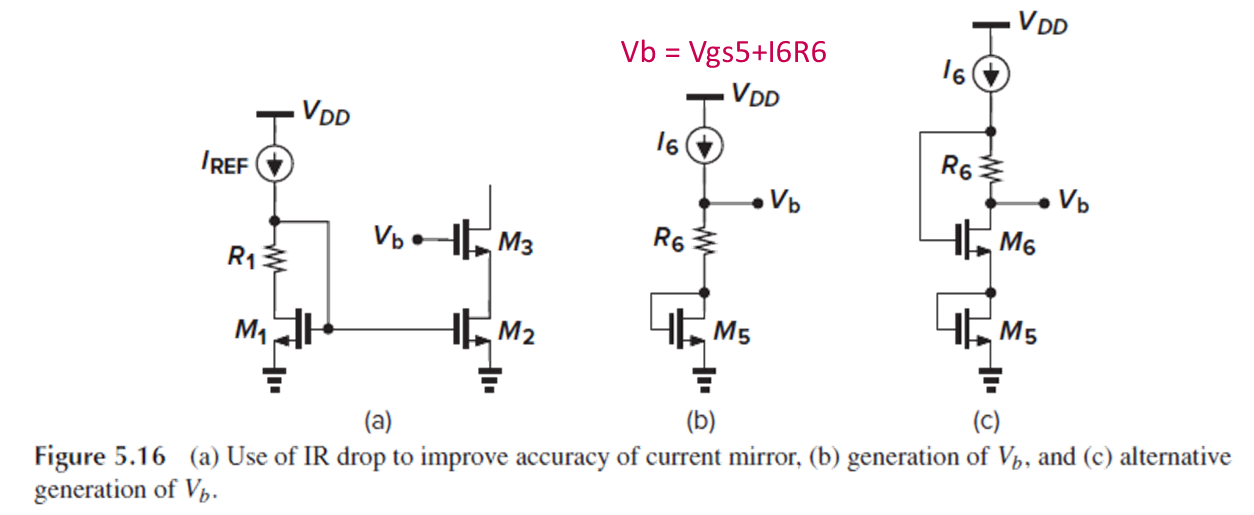
앞서 voltage headroom을 최대로 가져가려면 Vds2 = Vgs2-Vth2, Vb = Vgs3+(Vgs2-Vth2)여야 한다고 했었습니다.
이때, Vds1 = Vds2 (=Vgs2-Vth2)를 만들기 위해서, M1의 gate와 drain 사이에 저항을 삽입해서 gate와 drain 간의 전압 차이를 만드는 방법이 제시됩니다. (Fig. 5.16(a))
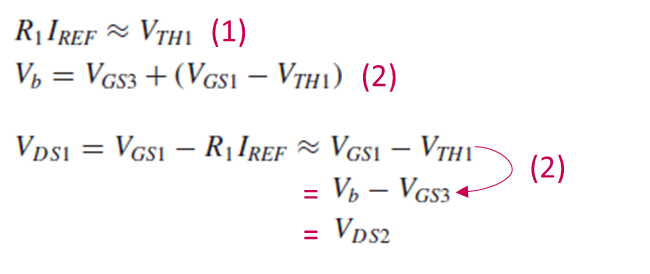
R1Iref ≈ Vth1인 R1과, Vb = Vgs3+(Vgs1-Vth1)인 Vb를 고르는 방법인데요.
그러면 Vds1 = Vgs1-R1Iref ≈ Vgs1-Vth1이 됩니다.
Vb = Vgs3+(Vgs1-Vth1)이므로 Vds1 = Vb-Vgs3이 되고, Fig. 5.16(a) 회로를 보면 이는 Vds2와 같죠.
이렇게, R1Iref ≈ Vth1인 R1과, Vb = Vgs3+(Vgs1-Vth1)인 Vb를 고르면 Vds1 = Vds2임을 보였습니다.
그런데 Fig. 5.16(a) 회로는 두 가지 단점이 있습니다.
첫째로, R1과 Vth가 PVT variation의 영향을 받기 때문에 R1Iref ≈ Vth1임을 보장할 수 없습니다.
두 번째 단점은, Vb = Vgs3+(Vgs1-Vth1)를 만들기 어렵다는 겁니다.
Vb의 식 꼴로 보아, Vb를 만들려면 diode-connected device가 필요하겠죠.
Vb를 Fig. 5.16(b)의 회로로 만들 수 있는데요.
Diode인 M5의 drain에 저항 R6가 연결되어 있고, 전체 branch에 전류 I6가 흐르고 있습니다.
이때 Vb = Vgs5 + I6R6겠죠.
Vgs5 = Vgs3이도록 M5의 size를 정하고, I6R6 = Vgs1-th1이도록 I6를 정하면 Vb = Vgs3+(Vgs1-Vth1)가 될 겁니다.
(1) 식에 의해 I6R6 = Vgs1-Vth1 = Vgs1-R1Iref가 되어, I6R6+R1Iref = Vgs1이 됩니다.
그런데 I6R6+R1Iref = Vgs1을 맞추기가 어려운 것이 문제입니다.
I6R6는 Vgs1의 변화를 따라가지 않고, 따로 노는 값이기 때문입니다.
책에서는 I6R6가 Vgs1를 ‘track’하지 않는다, 즉, 추적하지 않는다고 표현했습니다.
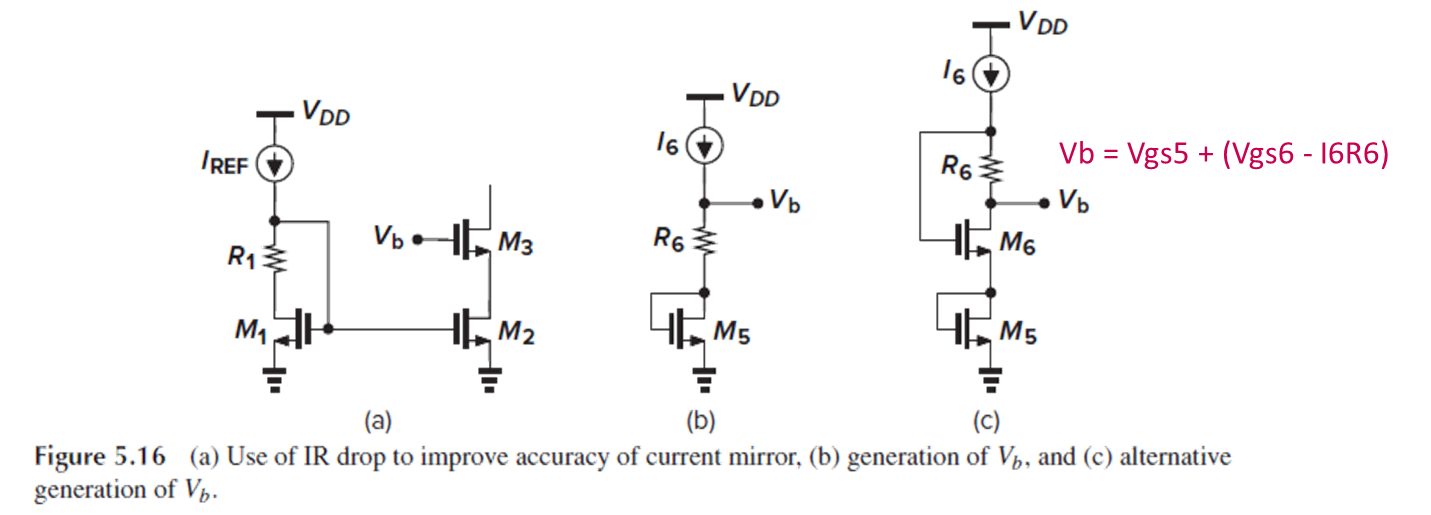
이 문제를 보완하는 회로가 Fig. 5.16(c)입니다.
Fig. 5.16(c)와 다른 점은, 저항 R6를 MOSFET M6의 gate와 drain 사이에 연결했다는 것입니다.
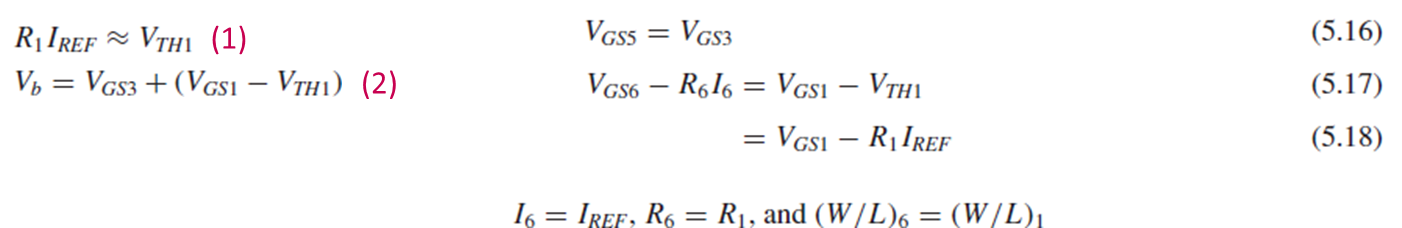
여기서는 Vb = Vgs5+(Vgs6-I6R6)이고, 이 식이 Vb = Vgs3+(Vgs1-Vth1)와 같도록 하기 위해서는 (5.16), (5.17), (5.18)을 만족해야 합니다.
아까와 달리, Vgs6-R6I6 = Vgs1-R1Iref를 만드는 것은 어렵지 않습니다.
I6 = Iref, R6=R1, (W/L)6 = (W/L)1 (Vgs6 = Vgs1)이도록 하면 쉽게 식을 만족시킬 수 있습니다.
그런데 second approach 회로의 발전은 여기서 끝나지 않습니다.
이번에는 low-voltage cascode라고도 불리는 회로를 볼 건데요.
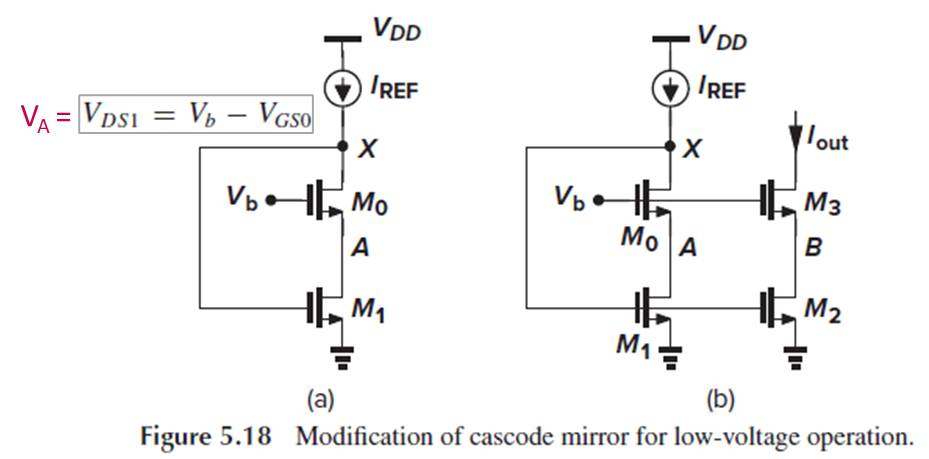
Fig. 5.18(a)를 보면, cascode의 input과 output을 서로 연결한 형태입니다.
Va = Vds1 = Vb-Vgs0이고, Vb는 M1이 saturation의 경계에 있도록 설정합니다.
이제 Fig. 5.18(b)와 같이, Iref를 생성하는 이 branch를 Iout을 복사하고자 하는 branch에 연결합니다.
그러면 Vgs0=Vgs3만 충족시키면, Vds1=Vds2가 되도록 할 수 있습니다.
Low-voltage cascode에서 Vb는 M1이 saturation의 경계에 있도록 설정한다고 했었습니다.
정확히는 M1과 M0가 모두 saturation에 있어야겠죠.
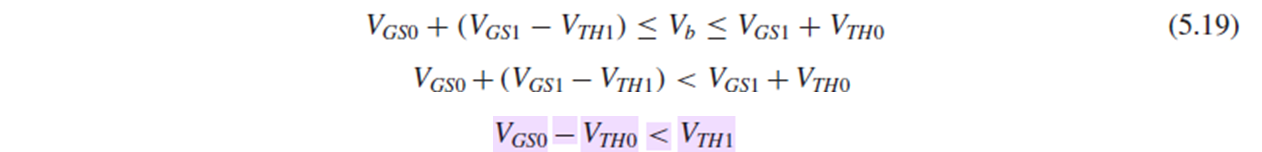
M0이 saturation되려면 Vgs0-Vth0 ≤ Vds0, 즉, Vb-Vth0 ≤ Vx(=Vgs1)여야 합니다.
M1이 saturaton되려면 Vgs1-Vth1 ≤ Vds1, 즉, Vgs1-Vth1 ≤ Va(=Vb-Vgs0)여야 합니다.
이 두 식을 연립해서 Vb의 범위를 (5.19)처럼 구할 수 있고, 이를 만족하기 위해서는 Vgs0-Vth0 < Vth1을 만족해야 합니다.
따라서, M0의 overdrive가 Vth1보다 작도록 M0의 sizing을 잘 해야 합니다.
그렇다면 이 Vb를 어떻게 만들어야 하는지 알아보겠습니다.
Voltage headroom을 최대로 가져가려면, Vds1 = Va = Vgs1-Vth1이어야 합니다.
그러기 위해서는 Vb가 Vgs0+(Vgs1-Vth1)과 같거나 살짝만 더 커야겠죠.
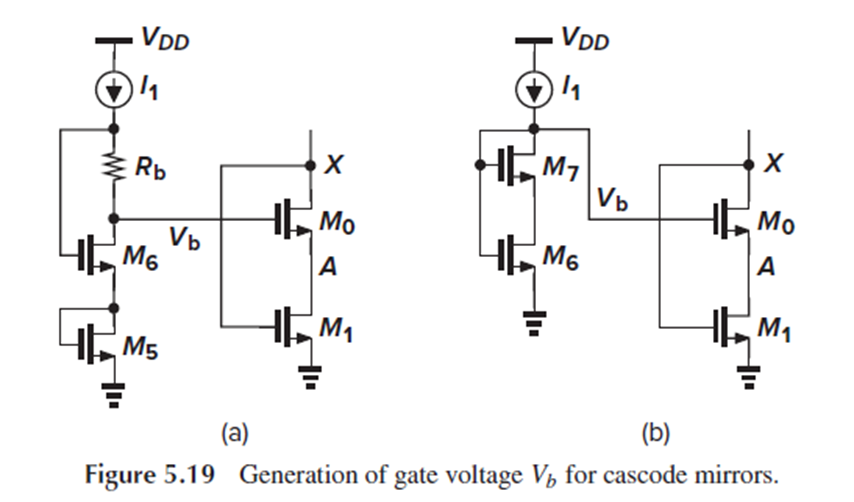
Fig. 5.19(a)와 같이 회로를 구성하면 됩니다.
상기하자면, 목표는 Vb ≈ Vgs0+(Vgs1-Vth1)이도록 하는 것입니다.
Fig. 5.19(a)에서 Vb = Vgs5+(Vgs6-RbI1)입니다.
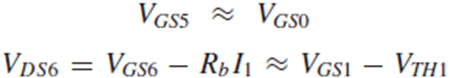
Vgs5 ≈ Vgs0, Vds6 = Vgs6-RbI1 ≈ (Vgs1-Vth1)이도록 하면 이는 우리가 목표하는 Vb ≈ Vgs0+(Vgs1-Vth1)와 같게 됩니다.
이 구조의 단점은, Vgs5 ≈ Vgs0를 만족해야 하는데, M5는 body effect가 없고, M0은 body effect가 생겨서 오차가 발생할 수 있습니다.
또한, RbI1값을 정밀하게 조절하기 힘듭니다.
그래서 Fig. 5.19(b)가 나은 방법이 될 수 있습니다.
이 회로에서 Vb = Vds6+Vgs7이므로, Vds6 ≈ Vgs0, Vgs7 ≈ (Vgs1-Vth1)이도록 설정하는 것이 좀더 쉽다고 합니다.
'CMOS IC Design' 카테고리의 다른 글
| Basic Differential Pair - 동작 특성, Common-Mode Behavior, Output Swing, Large-Signal & Small-Signal 분석, Half-Circuit Concept [Razavi][Ch4] (0) | 2024.11.18 |
|---|---|
| Single-Ended & Differential Signals [Ravazi][Ch4] (1) | 2024.11.18 |
| PVT(Process, Voltage, Temperature) Variation (1) | 2024.11.13 |
| Cascode Stage, Folded Cascode [Razavi][Ch3] (0) | 2024.11.13 |
| CG Stage(Common-Gate Stage) [Razavi][Ch3] (5) | 2024.11.05 |



