참고: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 4 - Differential Amplifiers (pg. 103~116)
4. Differential Amplifiers
4.2. Basic Differential Pair
Basic Differential Pair
Fig. 4.7의 basic differential pair 구조를 이용하면 Vout이 clipping되는 문제를 해결할 수 있습니다.

Fig. 4.6(a)와 달라진 점은, M1과 M2의 source를 묶어 tail current Iss를 달아준 것입니다.
Iss를 달아주면 Id1+Id2가 항상 Iss로 일정해지기 때문에, Id1+Id2가 Vin,cm에 independent하게 됩니다.
Vin1=Vin2이면, Id1=Id2=Iss/2가 되어, output common-mode가 Vdd-Rd*Iss/2가 됩니다.
Basic Differential Pair - Input-Output Characteristics
Id1+Id2=Iss라서, Vin1과 Vin2의 대소 관계에 따라 Vout1과 Vout2가 결정됩니다.
Output common-mode level은 Vin1=Vin2일 때의 Vout값인 Vdd-1/2*Rd*Iss로 정의됩니다.
Vin1-Vin2의 범위에 따른 Vout1과 Vout2의 변화 계산은 아래 그림을 참고하시길 바랍니다.

Vin1-Vin2에 따른 Vout1과 Vout2의 그래프가 Fig. 4.8(a)에 나타나 있습니다.
Vin-Vin2에 따른 Vout1-Vout2는 Fig. 4.8(b)와 같습니다.

이 그래프들로부터 differential pair의 특징을 파악할 수 있습니다.
Differential pair의 최대, 최소 output level이 각각 Vdd와 Vdd-Rs*Iss로 정확하게 정의되어 있습니다.
또, Fig. 4.8(b)가 (Vout1-Vout2) vs (Vin1-Vin2) 그래프라 기울기가 small-signal gain과 같은데, |Vout1-Vout2|가 0일 때 small-signal gain이 최대이고, |Vout1-Vout2|가 커질수록 small-signal gain이 0에 가까워지는 것을 볼 수 있습니다.
즉, input voltage swing이 커질수록 output voltage swing이 커지고, nonlinearity가 증가합니다.
* 회로에서 linearity는 Vin이 변해도 gain이 일정한 것으로 , Vout vs Vin 그래프에서 y=ax의 꼴인 구간이 회로가 linear한 구간입니다.
Basic Differential Pair – Common-Mode Behavior
이번에는 differential pair의 common-mode behavior를 보겠습니다.
Fig. 4.9(a)처럼 differential pair를 구성하는데, Iss를 NMOS로 구현하고 M1과 M2의 Vin을 둘다 Vin,cm으로 인가해 보겠습니다.
Input을 common-mode로 인가하면 M1, M2나 Vout에 의한 noise를 억제할 수 있습니다.

Vin,cm을 0부터 VDD까지 늘리면서 Id1, Id2, Vp, Vout1, Vout2의 변화를 보겠습니다.
i) Vin,cm=0
Id1=Id2=0이라, Id3=0입니다.
Vb가 M3에 inversion layer를 만들기에 충분하다 가정하면, M3는 deep triode region에서 동작하게 됩니다.
Id1=Id2=0이라 신호 증폭은 일어나지 않고, Vout1=Vout2=VDD라서 Vp=0입니다.
ii) Vin,cm≥Vth>0
Vin,cm을 증가시키다가, Vin,cm ≥ Vth가 되면 M1, M2가 켜집니다.
Id1과 Id2가 계속 증가해서 Vout1과 Vout2가 Vdd보다 작아집니다.
Fig. 4.9(b)처럼 M3를 Ron3로 모델링하면, Ron3에 흐르는 전류 Id1+Id2가 증가하니까 Vp는 증가합니다.
이 경우, M1과 M2가 source follower처럼 동작(Vin,cm이 input, Vp가 output)해서 Vp가 Vin,cm을 따라갑니다.
iii) 충분히 큰 Vin,cm
Vin,cm이 계속 커지면 Vp도 따라서 증가하다가, Vin,cm = Vgs1+(Vgs3-Vth3)에 도달하면 M3가 saturation region에서 동작하게 됩니다.
M3에 흐르는 전류인 Id1+Id2가 일정해져서, Id1, Id2가 일정해집니다.
즉, differential pair가 제대로 된 동작을 하려면 Vin,cm ≥ Vgs1+(Vgs3-Vth3)이어야 합니다.
iv) Vin,cm > Vgs1+(Vgs3-Vth3)
Vin,cm의 upper bound를 구해보려 합니다.
Vin,cm이 계속 증가하면, Vout1과 Vout2가 Vdd-1/2*Iss*Rd로 거의 일정한데 Vp는 source follower의 효과로 계속 Vin,cm을 따라 증가하게 됩니다.
Vout은 일정한데 Vp만 계속 증가하면 M1과 M2의 Vds가 계속 감소하다가 어느 시점부터는 M1과 M2가 triode region에서 동작하게 되겠죠.
그 경계값은 Vth의 값에 따라 Vdd-Rd*Iss/2+Vth 또는 Vdd 입니다.
따라서 differential pair가 제대로 동작하기 위한 Vin,cm의 범위는 (4.1)과 같습니다.
Vin,cm이 upper bound를 넘으면, Fig. 4.9(c)의 특성이 변하지는 않지만, differential gain이 감소합니다.
Basic Differential Pair – Small-Signal Gain

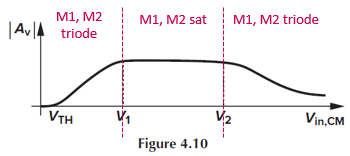
Differential gain을 구하는 example인데, 솔루션에 정확한 Av 공식은 나와있지 않아서, 정성적으로 알아두면 될 것 같습니다.
M1과 M2가 saturation일 때 small-signal differential gain이 일정하게 유지되어, 회로가 linear합니다.
Basic Differential Pair – Output Swing
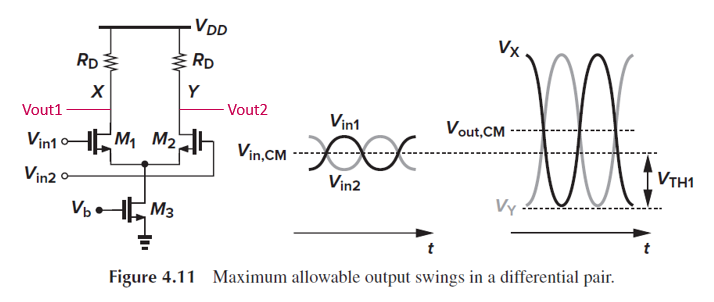
Differential pair의 output swing을 따져보겠습니다.
M1과 M2가 saturation이려면, Vout은 최대 Vdd, 최소 약 Vin,cm-Vth여야 합니다.
Input common-mode level(Vin,cm)이 낮을수록, 가능한 output swing이 커집니다.
여기서 M3의 saturation 조건도 고려하면, Vin,cm을 낮추더라도 Vgs1+(Vgs3-Vth3)보다 낮으면 안 되겠죠.
Basic Differential Pair - Large-Signal Behavior
Vin1-Vin2에 따른 Vout1-Vout2를 알아보면 differential pair의 large-signal behavior를 알아낼 수 있습니다.
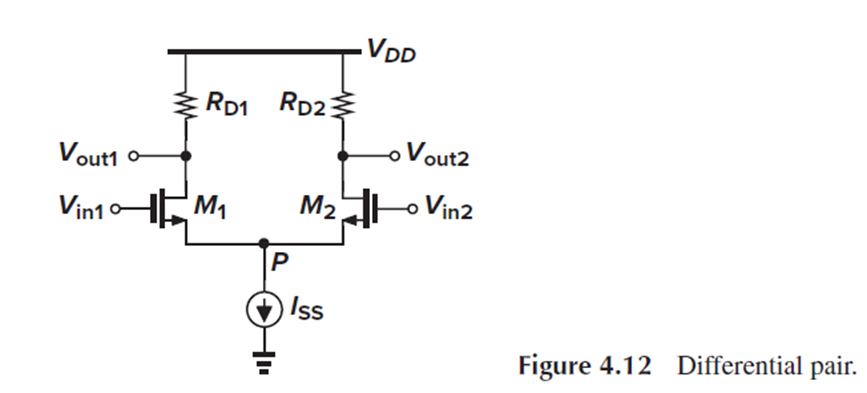
- Vin1-Vin2에 따른 Vout1-Vout2 찾기
Vout1 = Vdd-Rd1*Id1이고, Vout2 = Vdd-Rd2*Id2인데, Rd1=Rd2=Rd라고 하면,
Vout1-Vout2 = Rd*(Id1-Id2)가 됩니다.
여기서 Id1과 Id2를 Vin1과 Vin2에 대한 식으로 나타내면, Vin1-Vin2와 Vout1-Vout2의 관계식을 얻을 수 있습니다.
Node P의 전압을 Vin1-Vgs1 또는 Vin2-Vgs2로 나타낼 수 있으므로,
Vin1-Vgs1 = Vin2-Vgs2이고, 정리하면 Vin1-Vin2 = Vgs1-Vgs2(4.2)입니다.
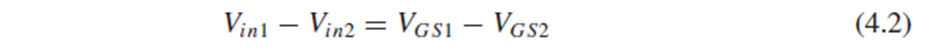
Saturation에 있는 MOSFET의 식(4.3) 을 Vgs에 대한 식으로 정리하고(4.4), (4.2)에 대입하면 (4.5)가 됩니다.
(4.5)의 양변을 제곱하면 (4.6)이 되고(Id1+Id2 = Iss), 식을 (4.7)과 같이 정리할 수 있습니다.
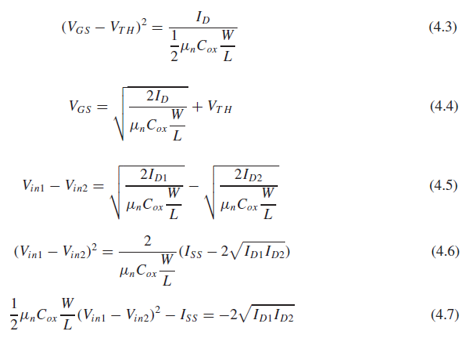
(4.7)의 양변을 제곱하는데, 4Id1*Id2를 Iss^2-(Id1-Id2)^2로 나타낼 수 있으므로, (4.8)을 얻을 수 있습니다.
식을 계속 정리하면 (4.10)의 Vin1-Vin2와 Id1-Id2에 대한 식을 얻을 수 있습니다.
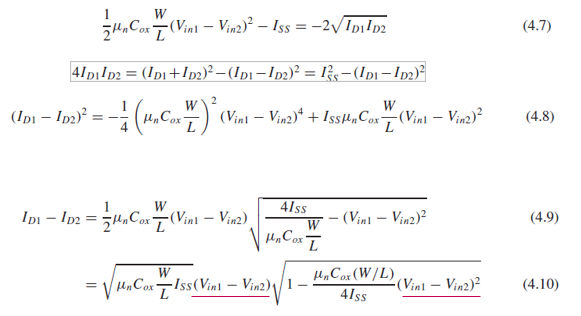
(4.10)으로부터, |Vin1-Vin2|가 증가할 때, Id1-Id2가 증가한다는 것을 알 수 있습니다.
루트 안의 (Vin1-Vin2)^2 감소량보다 루프 밖의 (Vin1-Vin2) 증가 효과가 더 크기 때문입니다.
- M1과 M2의 Equivalent Gm 구하기
Id1-Id2와 Vin1-Vin2를 각각 ΔId와 ΔVin으로 나타내고 Id를 Vin으로 편미분해서 (4.11)을 얻었습니다.
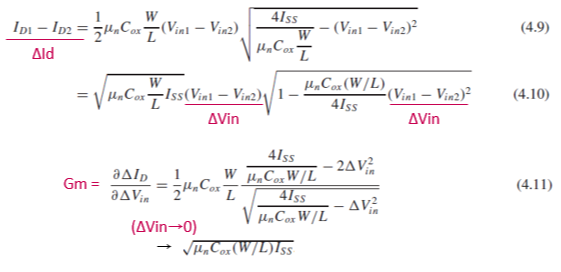
Differential pair가 대칭적으로 동작할 때 ΔVin→0이 됩니다.
따라서 equilibrium condition에서의 Gm은 (4.11)에 ΔVin→0을 대입한 값으로 구할 수 있습니다.
- Small-Signal Gain 구하기
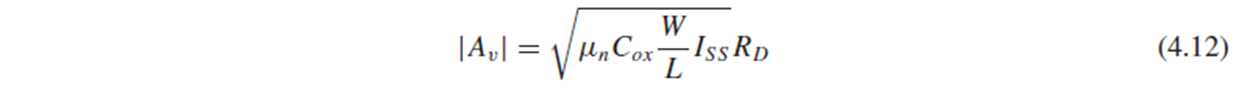
Vout1-Vout2 = Rd*ΔI = -Rd*Gm*ΔVin이므로, small-signal voltage gain |Av| = |ΔVout/Δvin| = Rd*Gm을 (4.12)과 같이 구할 수 있습니다.
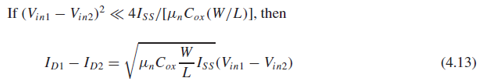
(4.9)에서 ΔVin << 4*Iss/[μnCox(W/L)]으로 Vin이 매우 작은 경우에도, 식이 (4.13)으로 되면서, 아까 ΔVin→0을 가정하고 구한 Gm과 같음을 확인할 수 있습니다.
- Differential Pair가 대칭적이지 않을 때의 Gm
ΔVin=0일 때, Gm은 (4.11)과 같았습니다.
그런데 만약 differential pair가 대칭적이지 않아 ΔVin이 커지면, 결론부터 말하면 Gm=0이 됩니다.
ΔVin이 커지다 보면 M1과 M2 중 하나는 꺼지고, 한쪽 branch에 Iss가 전부 흐르게 됩니다.
이렇게 되는 ΔVin을 ΔVin1이라고 하면, M2가 거의 꺼져 있고, Id1=Iss, Id2=0, ΔVin1=Vgs1-Vth가 되겠죠.
- (4.9)와 (4.10)은 M1과 M2가 둘다 saturation에 있을 때의 식이므로, M2가 완전히 꺼지면 성립하지 않습니다.
이때 ΔVin1=Vgs1-Vth의 값은 M1이 saturation일 때의 Id 식으로부터 (4.14)와 같습니다.
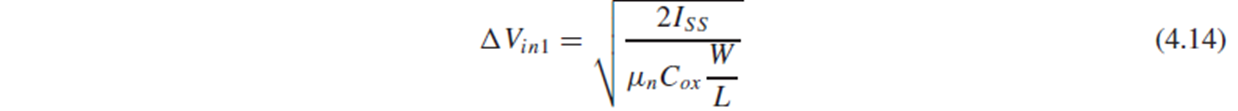
(4.14)를 Gm의 식 (4.11)에 대입하면, Gm=0이 됩니다.
그리고 ΔVin>ΔVin1이면 M2가 완전히 꺼져서 (4.9), (4.10)이 성립하지 않습니다.
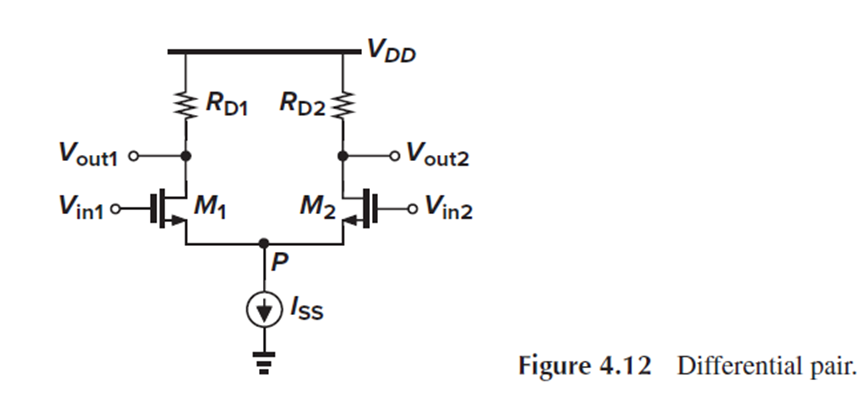
Vin에 따른 Id1과 Id2, Gm의 개형이 Fig. 4.13에 나타나 있습니다.

- W와 Iss가 변할 때의 Id1-Id2 변화 (Linearity 변화)
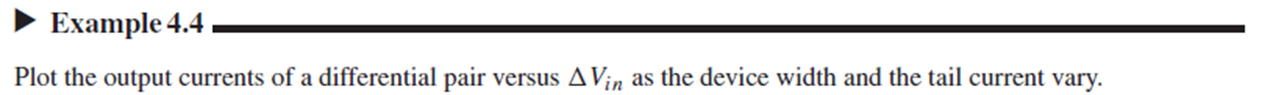
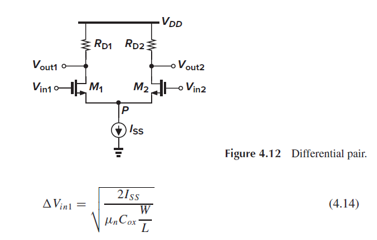
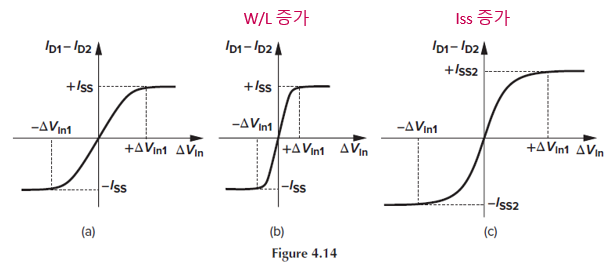
M1, M2의 W와 Iss가 변할 때, Id1-Id2 vs ΔVin의 그래프를 그리는 문제입니다.
(4.14)에 의해 W/L이 증가하면 Vin1이 감소하여 그래프가 Fig. 4.14(b)처럼 됩니다.
Iss가 증가하면 Fig. 4.14(c)처럼 Vin1이 증가하고, swing도 Iss2 ~ -Iss2로 증가합니다.
즉, differential pair에서 더 넓은 구간에서 linearity가 나타날 조건은 W/L가 감소하고, Iss가 증가하는 것입니다.
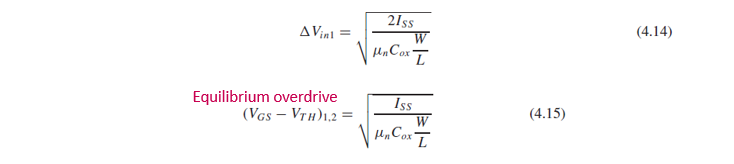
(4.14)의 ΔVin1 값은 M1과 M2 branch가 equilibrium일 때 M1과 M2의 overdrive voltage(4.15)의 루트2배입니다.
루트2배인 것 말고는 식의 형태가 같죠.
앞 example 4.4에서 봤듯 ΔVin1을 늘리면(W/L 감소 또는 Iss 증가) 회로가 linear하게 동작하는 구간이 늘어납니다.
그런데 주어진 Iss에 대해, linearity를 증가시키기 위해 W/L을 줄여 ΔVin1을 증가시키면 overdrive voltage도 증가합니다.
Fig. 4.14(b)의 반대의 상황이 되는 것인데, 이때 linearity는 좋아지지만, 그래프의 기울기인 gain은 작아집니다.
Basic Differential Pair - Small-Signal Behavior
- Large-Signal Behavior로부터 Small-Signal Gain 구하기
Basic differential pair의 small-signal behavior를 볼 건데, 우선 large-signal behavior의 결과로부터 small-signal differential voltage gain을 구해보겠습니다.
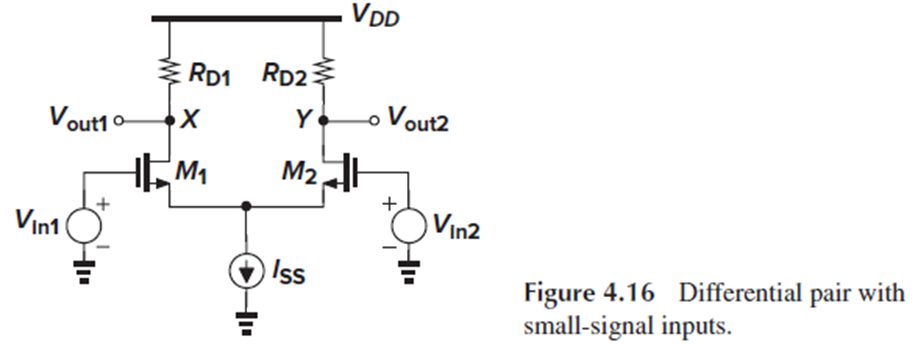
Differential pair에서 M1과 M2는 saturation region에 있고, Rd1 = Rd2 = Rd이라 가정하고,
small-signal input인 Vin1과 Vin2를 인가합니다.
Differential voltage gain은 앞서 large-signal behavior 부분에서 구한 (4.12)와 같습니다.
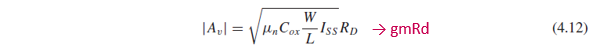
그런데 여기서 [μnCox(W/L)Iss]^(1/2)은 M1과 M2의 gm과 같습니다.
Equilibrium 근처에서 Id1=Id2=Iss/2이므로, gm 식에 Id=Iss/2를 대입하면 [μnCox(W/L)Iss]^(1/2)가 되기 때문입니다.
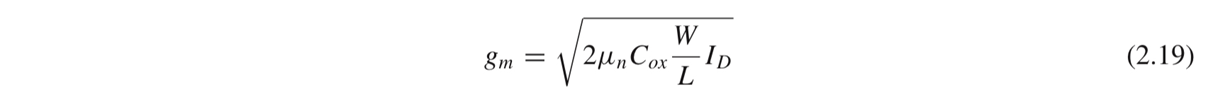
따라서 equilibrium 근처에서 differential voltage gain은 gmRd가 됩니다.
이제 small-signal analysis로 같은 결과가 나온다는 것을 보일 겁니다.
- Small-Signal Analysis(Method 1)
두 가지 방법을 알아볼 건데, 그 중 첫 번째 방법입니다.
Vin2를 0으로 두고, Vin1이 X와 Y, 즉 Vout1과 Vout2에 어떤 영향을 미치는지 보겠습니다. (Fig. 4.17(a))
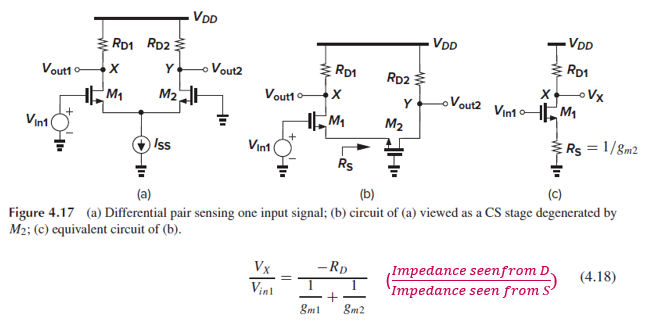
먼저 Vx/Vin1을 보자면, M1을 common source stage with source degeneration으로 볼 수 있습니다.
M2의 source에서 본 impedance만큼 source degeneration 되었다고 보는 겁니다. (Fig. 4.17(b))
M2의 source에서 본 impedance Rs는 1/gm2이고, 이걸 Fig. 4.17(c)처럼 CS stage 구조로 보기 편하게 그릴 수 있습니다.
CS stage with source generation의 voltage gain Vx/Vin1은 (4.18)과 같습니다.
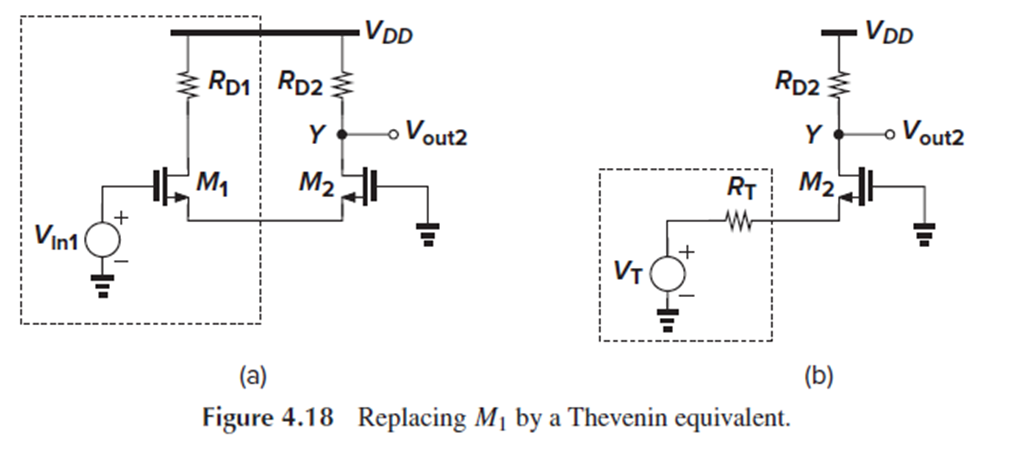
이번에는 Vy/Vin1을 구해보겠습니다.
Fig. 4.18(a)에서 Vin1과 M1을 thevenin equivalent로 대체하면 Fig. 4.18(b)가 됩니다.
Vt = Vin1, Rt = 1/gm1입니다.
Fig. 4.18(b)에서 M2가 common-gate stage로 동작하므로, gain Vy/Vin1은 (4.19)가 됩니다.
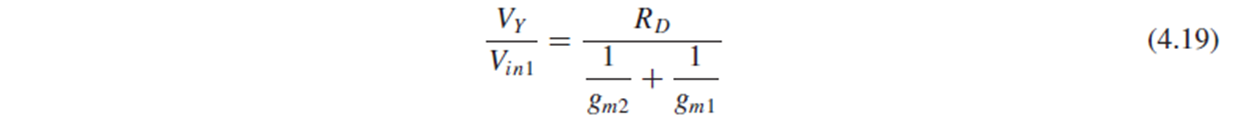
Vin1을 인가했을 때의 differential output voltage는 Vx-Vy이고, 이는 (4.18)과 (4.19)의 식을 뺀 (4.20)으로 구해집니다.
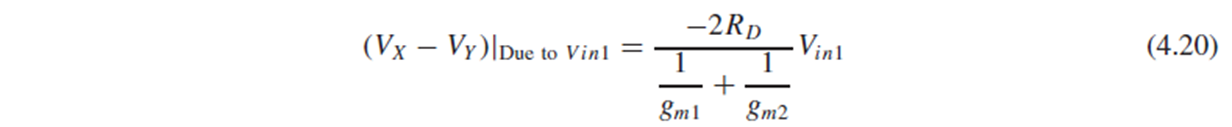
(4.20)에서 gm1=gm2=gm이면 (4.21)이 됩니다.
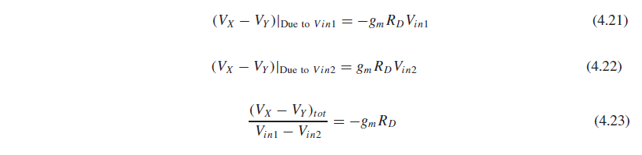
Symmetry에 의해, Vin2에 의한 Vx와 Vy의 변화는 Vin1에 의한 변화와 polarity만 반대입니다(4.22).
(4.21)과 (4.22)를 더하면, 전체 differential gain 식을 (4.23)과 같이 구할 수 있습니다.
만약 output이 single-ended였다면, 즉, output이 Vx-Vy가 아니라 Vx 또는 Vy였다면, gain은 ½배였을 겁니다.
- Small-Signal Analysis(Method 2)
Differential pair의 small-signal gain을 구하는 두 번째 방법입니다.
두 번째 방법에서는 lemma를 먼저 제시하고 이를 증명합니다.
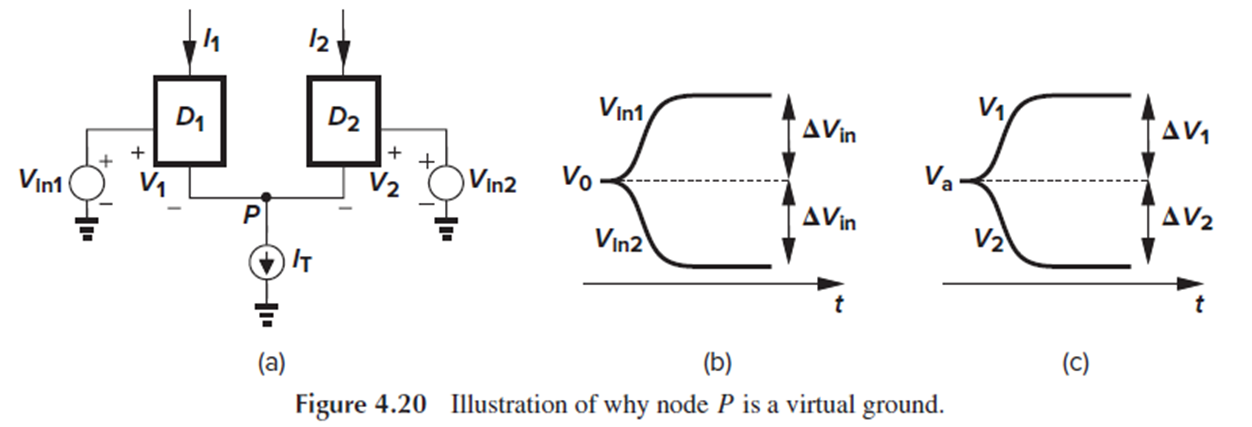
Fig. 4.20에서 D1과 D2는 임의의 3-terminal device입니다.
Lemma는 Vin1이 V0→V0+ΔVin, Vin2이 V0→V0-ΔVin으로 바뀔 때, “회로가 linear하게 작동한다면, Vp는 변하지 않는다“는 것입니다.
이 lemma에 대한 증명입니다.
해석 1)
회로가 linear하게 작동한다는 것은, I1-I2가 Vin1-Vin2에 선형적으로 비례한다는 뜻입니다.
그런데 I1-I2가 커지면, D1과 D2 중 saturation을 벗어나는 것이 생겨서 differential pair가 linear한 특성을 잃게 됩니다.
즉, linearity를 위해서는 I1-I2가 아주 작아야 하는데, I1과 I2가 거의 같다는 것은 Vp가 일정하다는 것과 같죠.
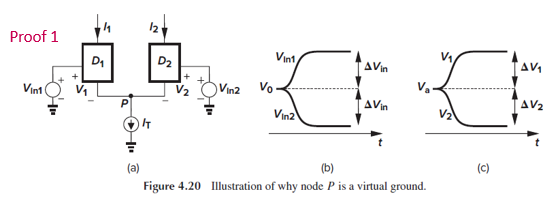
해석 2)
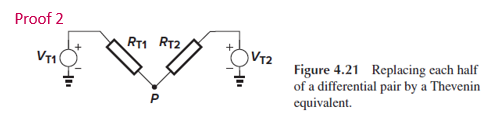
또는, Fig. 4.21처럼 node P에 D1과 D2가 미치는 영향을 각각 thevenin equivalent로 나타내서 증명할 수도 있습니다.
Vt1는 ΔVin만큼 변하고, Vt2는 -ΔVin만큼 변한다고 생각해 봅시다.
Vt1과 Vt2의 변화가 매우 작아서 1/gm1 =1/gm2라서 Rt1=Rt2일 때, Vp는 일정하게 유지됩니다.
해석 3)
가장 정석적인 증명입니다.
Fig. 4.20(c)처럼, V1과 V2가 equilibrium value Va를 중심으로 ΔV1과 ΔV2만큼 변한다고 생각해 봅시다.
또, 회로가 대칭적이라 D1과 D2가 동일한 gm을 가진다고 가정합니다.

그러면 I1은 gmΔV1, I2는 gmΔV2만큼 변할 것입니다.
I1+I2=It로부터 ΔV1 = -ΔV2를 얻을 수 있습니다.
또, 대칭적인 회로를 가정하므로 Vgs1=Vgs2, 즉, Vin1-V1 = Vin2-V2 입니다.
이 식을 bias와 변화량에 대한 식으로 나타내고 ΔV1 = -ΔV2를 대입하면, ΔVin = ΔV1 을 얻을 수 있습니다.
이게 무슨 의미를 갖냐면, Vin1과 Vin2가 각각 ΔVin과 –ΔVin만큼 변할 때, output인 V1과 V2도 각각 ΔVin과 –ΔVin만큼 변한다는 것입니다.
Vp = Vin1-V1인데, Vin1과 V1의 변화량이 같으므로, Vp는 일정하게 유지된다는 결론이 납니다.
Half-Circuit Concept
Vin과 Vout의 변화에도 Vp가 일정하기 때문에, Vp를 “ac ground”, 혹은 “virtual ground”라 부릅니다.
Small-signal 관점에서는 Fig. 4.22(b)처럼 node P를 gnd로 보는 것입니다.
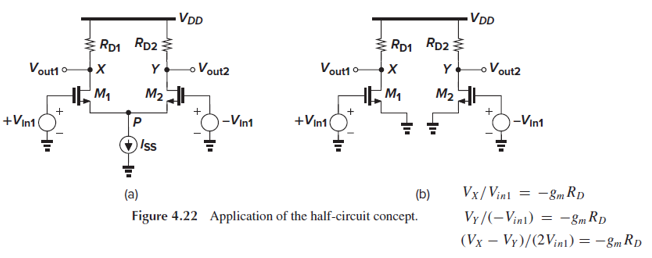
그러면 양쪽 branch를 별개의 회로로 볼 수 있는데, 이를 “half-circuit concept”라고 합니다.
양쪽 branch 각각의 gain인 Vx/Vin1과 Vy/(-Vin1)은 모두 –gmRd입니다.
따라서, 전체 small-signal differential gain인 (Vx-Vy)/(2Vin1) = -gmRd입니다.
Half-circuit concept는 symmetric differential pair에 fully differential input이 가해질 때의 회로 분석에 용이합니다.
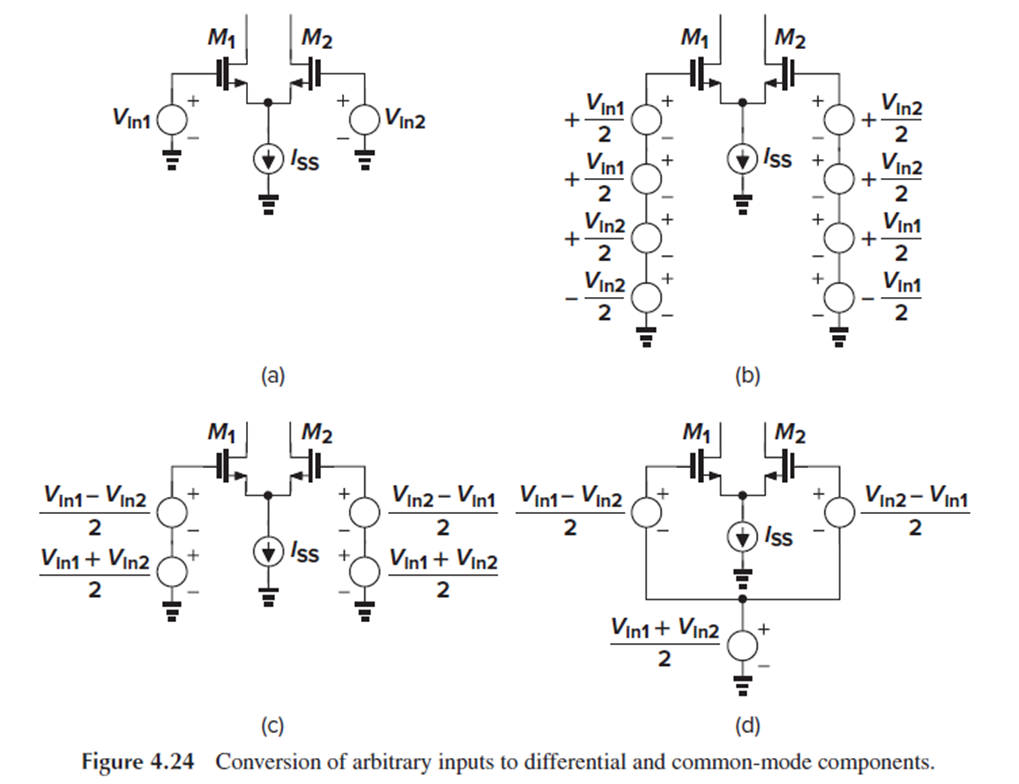
이번에는 Fig. 4.24(a)처럼 half-circuit concept에서 두 input이 fully differential하지 않을 때, 즉, input이 같은 양만큼(ΔVin, –ΔVin) 변하지 않을 때는 회로를 어떻게 분석하는지 알아보겠습니다.
Fig. 4.24(b)처럼 Vin1과 Vin2를 각각 (Vin1/2+Vin1/2)+(Vin2/2-Vin2/2), (Vin2/2+Vin2/2)+(Vin1/2-Vin1/2)로 보면,
Fig. 4.24(c)처럼 Vin1과 Vin2를 각각 (Vin1-Vin2)/2+(Vin1+Vin2)/2, (Vin2-Vin1)/2+(Vin1+Vin2)/2로 나타낼 수 있겠죠.
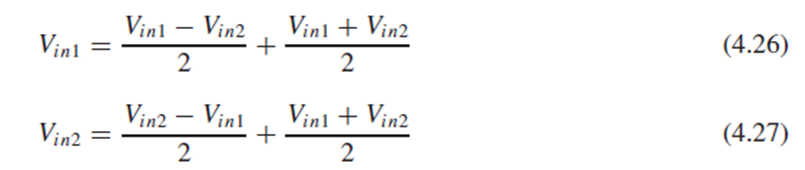
(Fig. 4.24(d)) Vin1과 Vin2에서 공통되는 (Vin1+Vin2)/2를 묶어주고, (Vin1-Vin2)/2와 (Vin2-Vin1)/2를 분리해서 Vin1과 Vin2를 나타낼 수 있습니다.
공통되는 부분과 다른 부분을 Fig. 4.25처럼 분리해서 나타낼 수 있습니다.
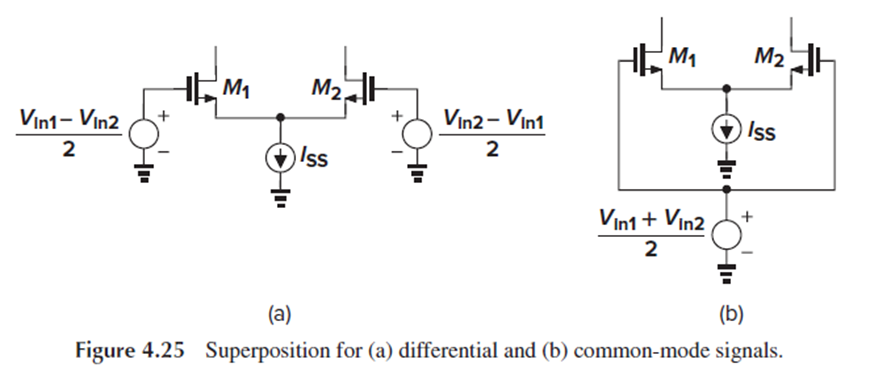
Fig. 4.25(b)의 공통되는 부분이 Vin,cm이 되고, Fig. 4.25(a)의 두 input이 fully-differential합니다.
여기서 fully-differential한 Fig. 4.25(a)에만 half-circuit concept를 적용해서 양쪽 회로를 분리해 분석하면 됩니다.
'CMOS IC Design' 카테고리의 다른 글
| Differential pair with MOS Loads, Gilbert Cell [Razavi][Ch4] (0) | 2025.01.07 |
|---|---|
| Degenerated Differential Pair, Common-Mode Rejection Ratio(CMRR) [Razavi][Ch4] (0) | 2024.11.19 |
| Single-Ended & Differential Signals [Ravazi][Ch4] (1) | 2024.11.18 |
| Current Mirrors(Basic, Cascode) [Ravazi][Ch5] (2) | 2024.11.13 |
| PVT(Process, Voltage, Temperature) Variation (1) | 2024.11.13 |



