참고: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 3 - Single-Stage Amplifiers (pg. 68~75)
3.4. Source Follower
Source Follower
앞서 알아본 CS stage의 voltage gain은 –gm*(load impedance)였습니다. (gm: Vin을 인가하는 MOSFET의 gm)
그래서 높은 voltage gain을 얻으려면 load impedance가 커야 합니다.
만약 low impedance load가 달려 있다면, amplifier 뒤에 buffer를 붙여 gain의 손실을 막아야 합니다.
이때 voltage buffer 역할을 할 수 있는 게 “common drain stage”로, 책에서는 계속 “source follower”라고 부릅니다.

Fig. 3.34(a)의 source follower를 보면, source follower는 신호를 gate로 받아들이기 때문에, input impedance가 높습니다.
그리고 load가 source에 연결돼 있어서, source 전압이 gate 전압을 “follow”할 수 있습니다.
Fig. 3.34(b)는 CS stage의 outut을 input으로 받는 source follower가 어떻게 CS stage의 voltage gain을 떨어뜨리지 않으면서도, 작은 저항을 drive할 수 있는지 보여줍니다.
2) Vin > Vth이면 M1이 ‘on’ 되면서 saturation region에 들어가, Rs에 Id1이 흐르게 됩니다.
3) Vin이 Vth를 넘어 계속 커지면, Vout은 Vin과 Vgs만큼의 간격을 두고 Vin을 따라갑니다.
여기서 세 가지 의문을 제기할 수 있습니다.
Q1) Vgs는 일정한 값인가?
A1) Fig. 3.34(c)에서는 Vgs가 일정하게 그려졌지만, 실은 bias current가 일정한 경우를 제외하고 Vgs는 일정하지 않습니다.
Q2) M1이 켜지는 정확한 조건은 Vgs = Vin-Vout > Vth인데 왜 Vin > Vth라고 단순화하는 건지?
A2) M1이 켜지는 순간에는 Vout=0이기 때문입니다.
Q3) 왜 M1이 켜지는 순간 saturation 되는 건지?
A3) M1의 saturation 조건은 Vds > Vgs-Vth → Vdd-Vout > (Vin-Vout)-Vth → Vdd > Vin-Vth입니다.
Vdd는 회로에서 가장 큰 값이기 때문에 Vdd > Vin-Vth가 항상 성립합니다.따라서 M1이 켜지기만 하면 saturation region에서 동작하게 되는 겁니다.
Source Follower의 Input-Output 특성


Source follower의 Vout은 Id1*Rs와 같으며, (3.82)로나타낼 수 있습니다.
여기서는 channel-length modulation은 무시되었습니다.
Source follower의 small-signal gain을 얻기 위해 (3.82)의 양변을 Vin으로 미분하고(3.83), chain rule에 의해 식을 정리하고(3.84), gm으로 정리했습니다(3.85).



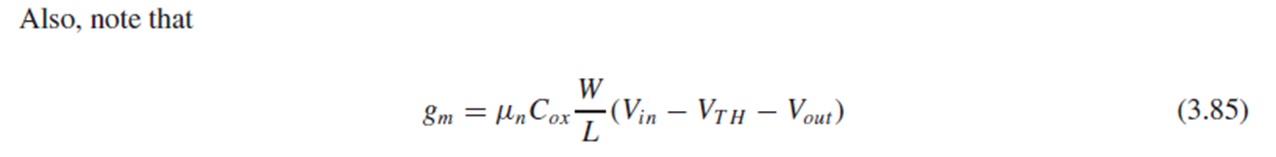

그 결과, source follower의 small-signal gain으로 (3.86)의 식을 얻습니다. (η: 에타)
Small-signal equivalent circuit으로도 같은 결과를 얻을 수 있습니다.
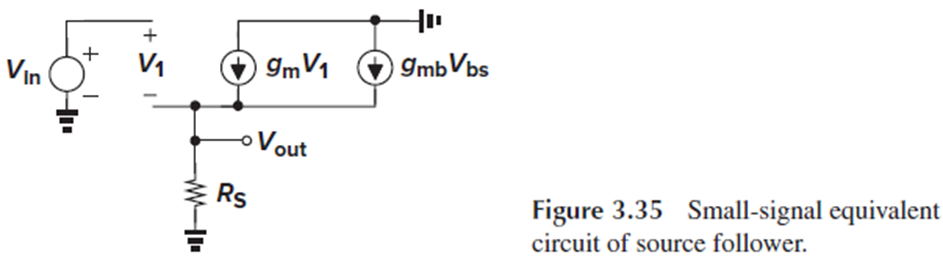
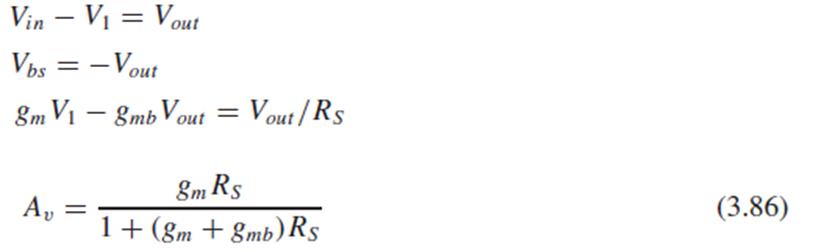
Source Follower의 Voltage Gain
Source follower의 Vin에 따른 voltage gain 그래프는 Fig. 3.36과 같습니다.
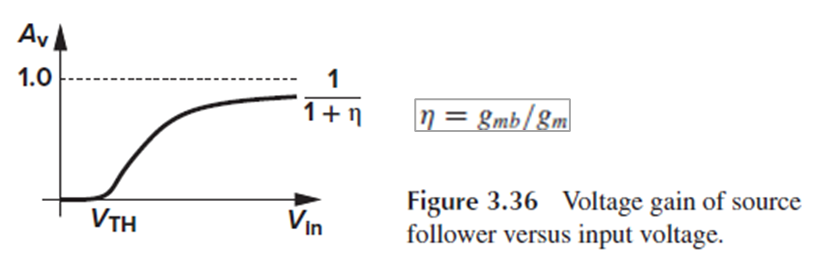
Vin≈Vth일 때는 MOSFET이 완전히 켜지지 않으므로, Id가 거의 흐르지 않아, gm=∂Id/∂Vgs≈0입니다.
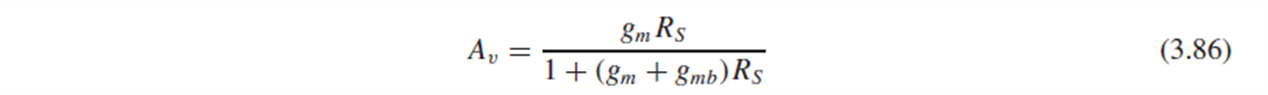
(3.86)에 gm=0을 대입하면, 이때의 voltage gain이 0임을 알 수 있습니다.
Vin>Vth이 되면 Id와 gm이 증가해서, voltage gain이 gm/(gm+gmb) = 1/(1+η)에 다가갑니다.
분자, 분모를 gmRs로 나누고 gmRs>>1이라고 하면 Av=1/(1+η)이 됩니다.
여기서 알아둬야 할 것이, Rs=∞가 되더라도, body effect가 제거되지 않는 이상 source follower의 voltage gain은 1이 될 수 없다는 것입니다.
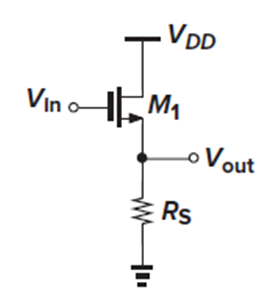
Source Follower using a Current Source
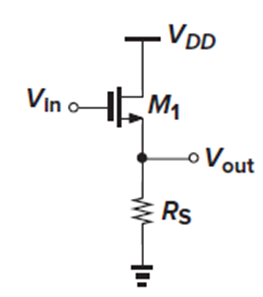
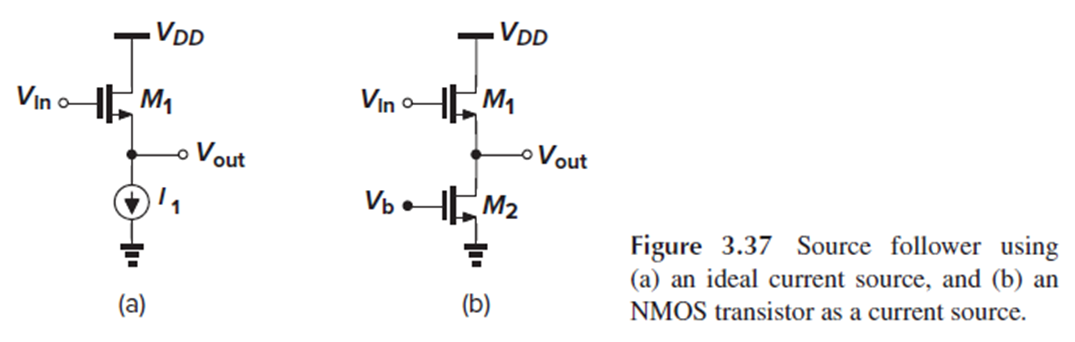
왼쪽의 source follower에서는 M1의 drain current가 Vin의 dc level에 강하게 의존합니다.
예를 들어, Vin이 0.7V에서 1V로 바뀔 때 Id가 2배 증가한다면, Vgs-Vth는 루트2배만큼 증가하게 됩니다.
Vth가 비교적 일정하다고 해도, Vgs가 증가한다는 것은 Vout = Vin-Vgs가 Vin을 일정하게 따라가지 못하게 되는 것이죠.
이렇게 되면 회로의 nonlinearity가 증가하게 됩니다.
이 의존성을 완화하기 위해, source에 연결된 resistor를 current source로 바꾼 것이 Fig. 3.37(a)의 회로입니다.
Current source는 saturation region에서 동작하는 NMOS로 구현되었습니다. (Fig. 3.37(b))
Example 3.13
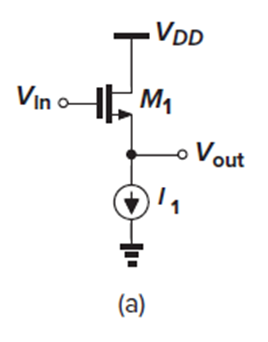
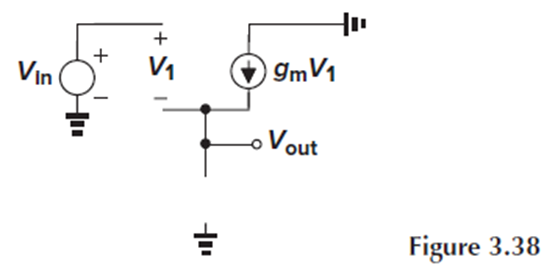
Fig. 3.37(a)의 source follower(왼쪽 그림)에서 I1이 ideal하고 λ=γ=0일 때 (channel-length modulation과 body effect를 무시할 때) 왜 gain이 unity(=1)인지 설명하라는 문제입니다.
Source follower의 source에 저항 대신에 current source가 달려있을 때 왜 Vin=Vout인지 설명하라는 문제인데요.
이 경우, large-signal 관점에서는 current source에 의해 M1의 drain current인 Id1이 I1으로 일정하므로, Vgs1도 일정합니다.
Fig. 3.38의 small-signal model에서, I1이 ideal하므로 input resistance가 ∞라 open입니다.
결국 small-signal drain current가 흐를 수 있는 경로가 없어 small signal Id=0이 되며, V1=0, Vout=Vin이 됩니다.
Source Follower의 Output Resistance
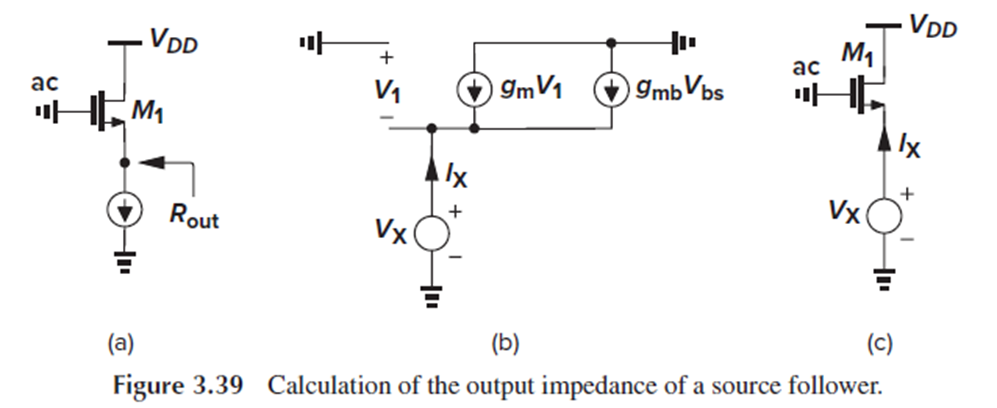
Fig. 3.39(a)의 source follower의 small-signal output resistance를 구해보겠습니다.
Fig. 3.39(b)의 small-signal equivalent circuit에서 Vx= -Vbs = -V1입니다. Bulk는 gnd에 연결되니까요.
Source node에서 KCL을 적용하면 (3.90)가 되고, 이로부터 Rout=Vx/Ix를 구하면 (3.91)입니다.
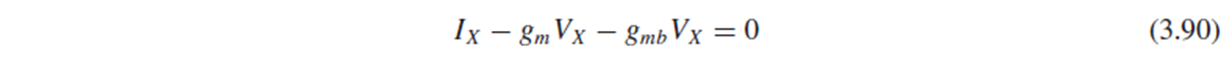
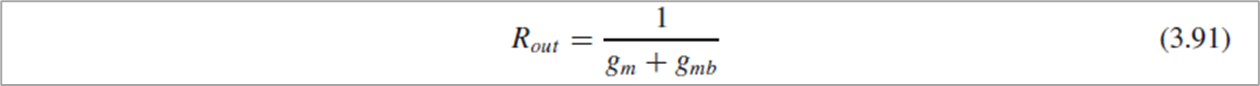
여기서 흥미로운 사실은, body effect가 source follower의 output resistance를 감소시킨다는 것입니다.
이를 이해하기 위해, Fig. 3.39(c)에서 Vx가 ∆V만큼 감소해서 Id1이 증가했다고 가정해 봅시다.
Test voltage Vx에 의해 생성된 test current Ix는 Id1과 반대 방향으로 흐르고 있었는데, Vx와 Ix가 감소하면 Id1이 증가하겠죠.
Body effect가 없다면, Id1이 증가함에 따라 M1의 Vgs가 ∆V만큼 증가할 것입니다.
반대로 body effect가 있다면, Vsb가 감소하여 Vth가 감소하는 효과가 더해지겠죠.
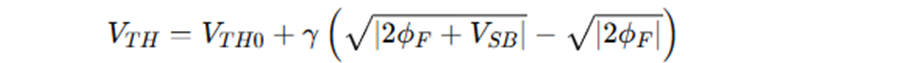
따라서, body effect가 있을 때 Id 식의 (Vgs-Vth)^2에서 Vgs는 증가하고 Vth는 감소해서, Id 변화가 증가하여 gm이 커지므로 Rout은 감소하게 됩니다.
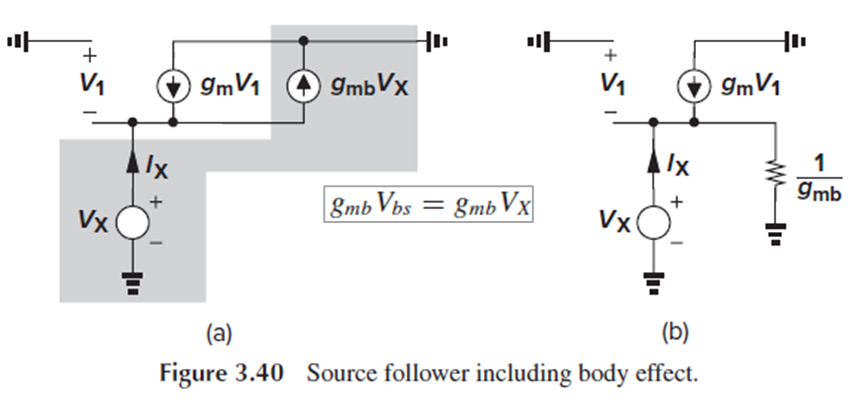
이 현상은 Fig. 3.40(a)의 small-signal model로도 관찰할 수 있습니다.
Fig.3.39(b)서 current source에 흐르는 gmbVbs를, Fig. 3.40(a)에서는 반대 방향으로 흐르는 gmbVx로 바꾸어 표기했습니다.
회색으로 표시한 부분에서 gmbVx는 등가저항 1/gmb 로 바꾸어 그릴 수 있습니다.
이 저항에 흐르는 전류가 Vx/(1/gmb)=gmbVx로, current source 값과 동일하기 때문입니다.
이 등가저항은 output과 병렬로 나타나며, output resistance를 떨어뜨립니다.
Output resistance 식은 (3.92), (3.93)로 나타납니다.
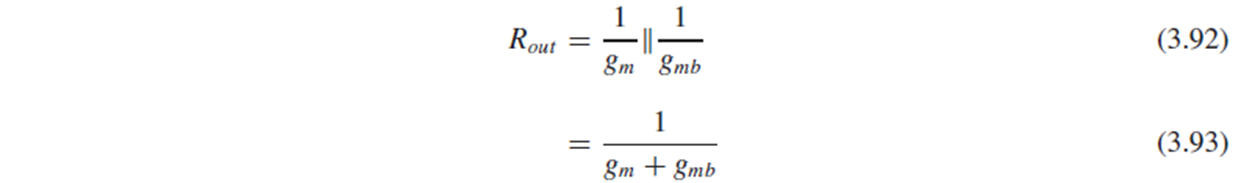
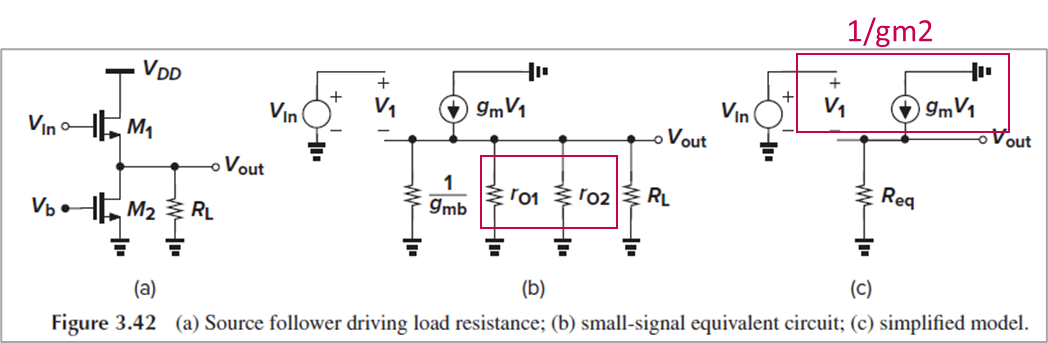
Source Follower with Load Resistance
이번에는 finite load resistance와 channel-length modulation을 가진 source follower를 봅시다.
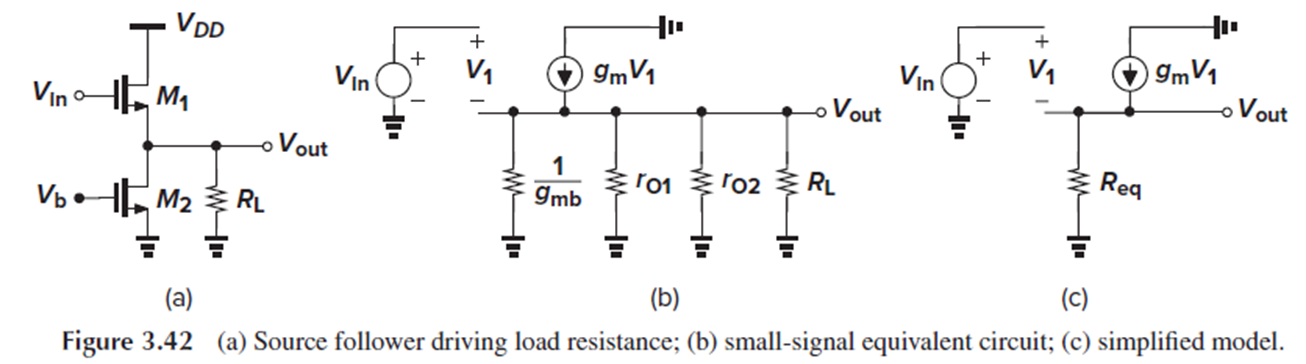
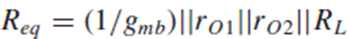
Fig. 3.42(b)에서 병렬인 저항들을 Fig. 3.42(c)에서는 하나의 등가저항 Req로 표현했습니다.
마찬가지로 Vout 윗부분의 output resistance는 1/gm이므로, voltage gain은 (3.96)처럼 나타납니다.
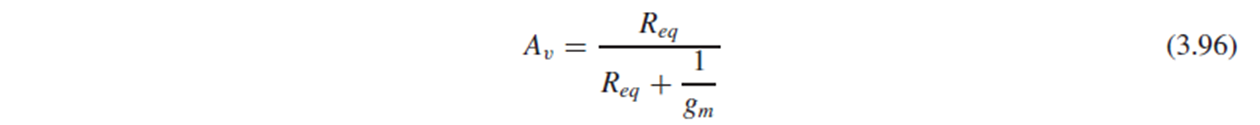
Example 3.14
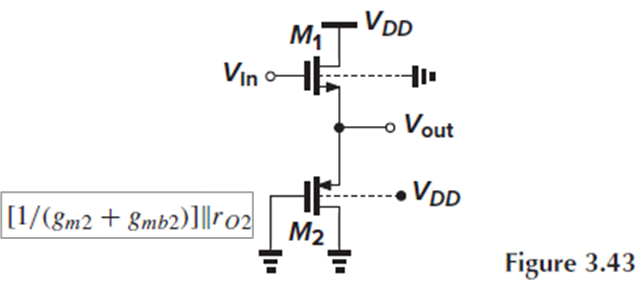
Fig. 3.43 속 source follower의 voltage gain을 구해야 합니다.
이 회로의 경우, source에 연결된 pmos M2의 gate는 gnd, bulk는 VDD에 연결되어 있습니다.
M2의 source와 gate 전압이 같으므로, diode-connected device이죠.
M2의 source에서 본 impedance가 [1/(gm2+gmb2)] || ro2입니다.
M1의 source에서 본 impedance는 ro1 || 1/gmb1이므로, (3.96)에서의 Req가 [1/(gm2+gmb2)] || ro2 || ro1 || 1/gmb1입니다.
이를 위의 (3.96)에 대입하면 (3.97)를 voltage gain으로 얻습니다.
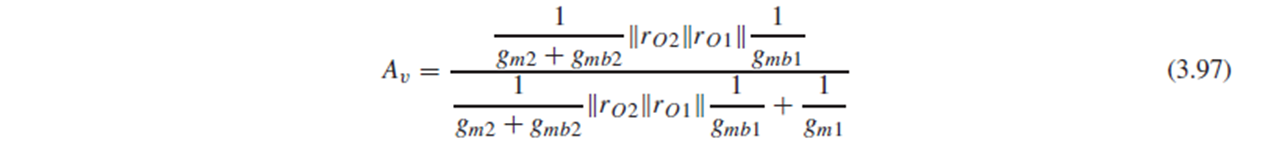
Source Follower의 단점
Source follower는 높은 input impedance와 적당한 output impedance를 낸다는 장점이 있지만, 두 가지 단점이 있습니다.
바로 nonlinearity와 voltage headroom 제한입니다.
우선 첫 번째, nonlinearity부터 살펴봅시다.
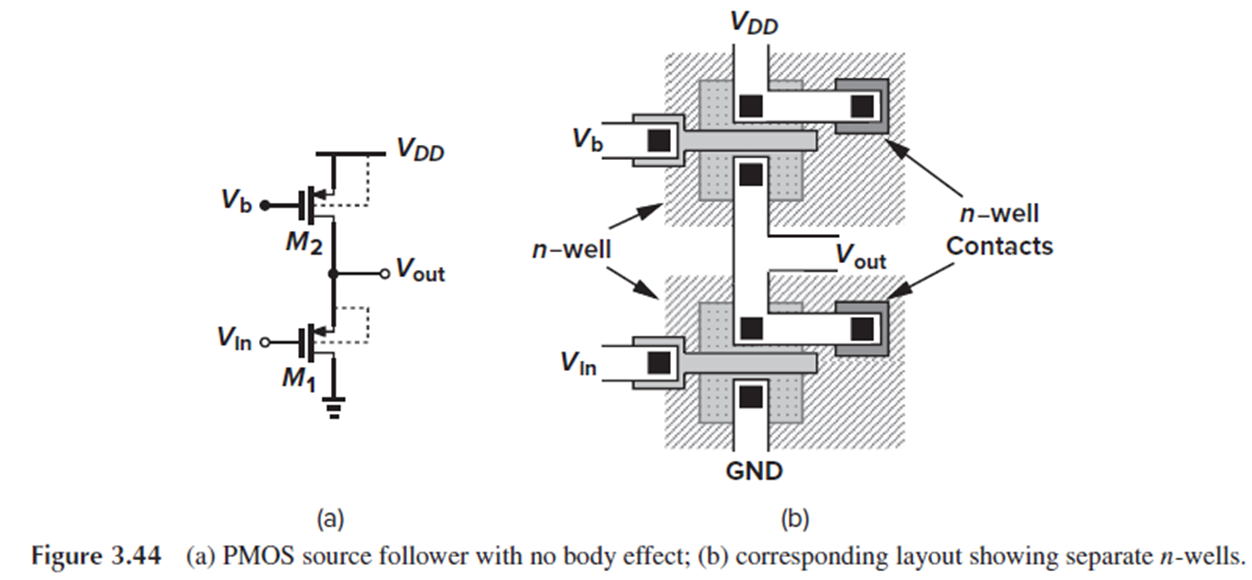
Fig. 3.44(a)에서 볼 수 있듯, source follower(M1)가 아무리 ideal한 current source에 의해 bias되었다 해도, body effect로 인해 Vth가 Vs에 nonlinear하게 의존하기 때문에 회로 특성이 nonlinear할 수밖에 없습니다.
또한, feature가 작은 공정에서는 ro가 Vds 변화에 의해 상당히 변하면서 small-signal gain에 추가적인 변화를 가져옵니다.
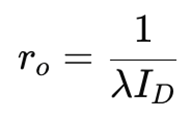
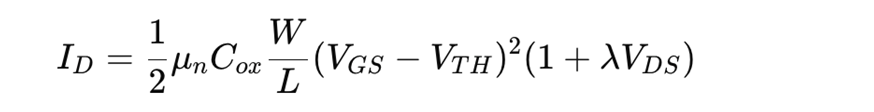
그렇다면 이 nonlinearity를 어떻게 없앨 수 있을까요?
Body effect로 인한 nonlinearity는 bulk를 source에 연결하면 없앨 수 있습니다.
이는 NMOS에서는 안 되고, PMOS에서만 쓸 수 있는 방법입니다.
모든 NMOS는 같은 substrate를 공유하기 때문입니다.
Figure 3.44(b)는 PMOS source follower에서 2개의 n-well을 따로 만들어서 PMOS M1의 body effect를 제거하는 것을 보여줍니다.
Source follower를 이렇게 PMOS로 만들면 nonlinearity는 줄일 수 있지만, mobility가 NMOS보다 낮아 NMOS source follower보다 output impedance가 높아집니다.
둘째, voltage headroom 제한입니다.
Source follower는 신호의 dc 레벨을 Vgs만큼 shift하기도 합니다.
따라서 voltage headroom과 voltage swing을 제한하게 됩니다.
이를 이해하기 위해, Fig, 3.45의 예시를 생각해 봅시다.
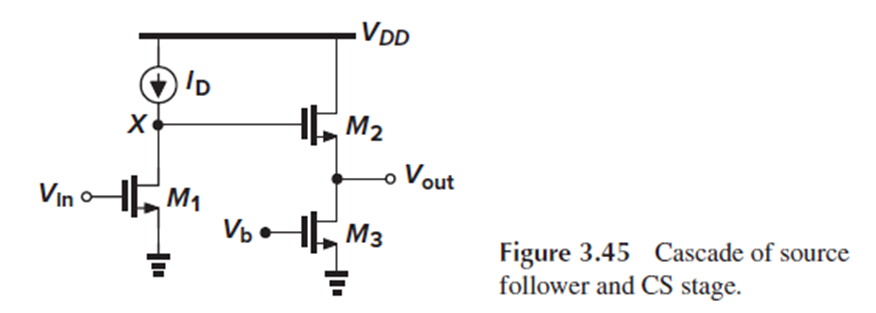
Source follower가 없었다면, M1이 saturation에 있도록 하는 최소 Vx는 Vgs1-Vth1였을 겁니다.
그런데 source follower를 연결하면, M3이 saturation에 있게 하기 위해서는 Vx가 Vgs2+(Vgs3-Vth3)보다 커야 합니다.
M1과 M3의 overdrive voltage(Vgs-Vth)가 비슷하다면, source follower를 연결함으로써 X에서의 가능한 swing이 Vgs2만큼이나 줄어들게 된다는 것을 의미합니다.
Source Follower vs CS Stage
이번엔 load impedance가 낮을 때 source follower와 common source stage의 gain을 비교해 보겠습니다.
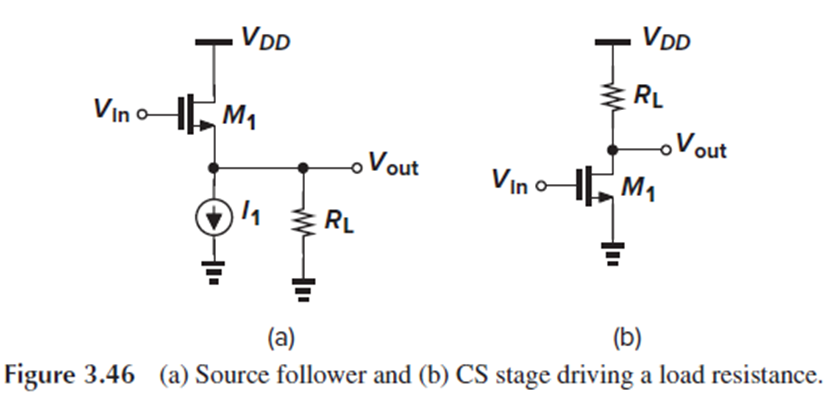
Fig. 3.46(a)는, load RL이 (3.99)의 voltage gain으로 source follower에 의해 drive되고 있는 상황입니다.
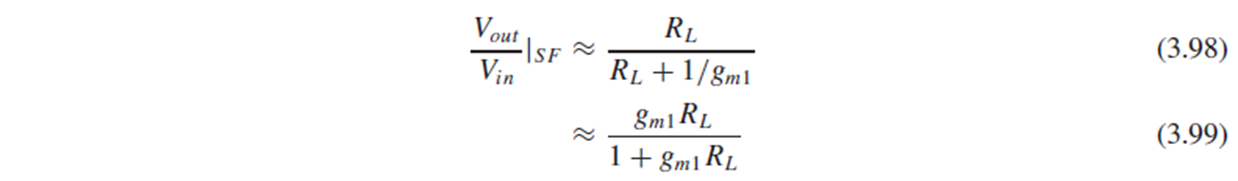
Fig. 3.46(b)에서는 RL이 (3.100)의 gain을 가진 common source의 load입니다.
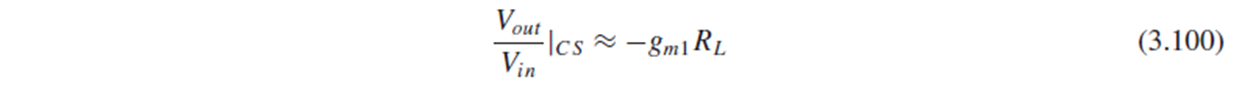
이 두 경우의 주요한 차이는, 주어진 bias current로 얻을 수 있는 voltage gain입니다.
예를 들어, 1/gm1≈RL이라면 source follower는 0.5의 gain을 얻을 수 있고, CS stage는 1에 가까운 gain을 얻을 수 있습니다.
Source follower가 driving을 그리 효율적으로 하는 amp는 아니라는 거죠.
앞서 살펴본 nonlinearity와 voltage headroom 제한의 문제 이외에도, driving도 잘 하지 못하기 때문에, source follower는 꼭 필요한 경우가 아니라면 쓰지 않습니다.
그렇다면 source follower가 필요한 경우는 어떤 경우일까요?
바로 voltage-level shift를 수행할 때입니다.
Source Follower - Voltage-Level Shift
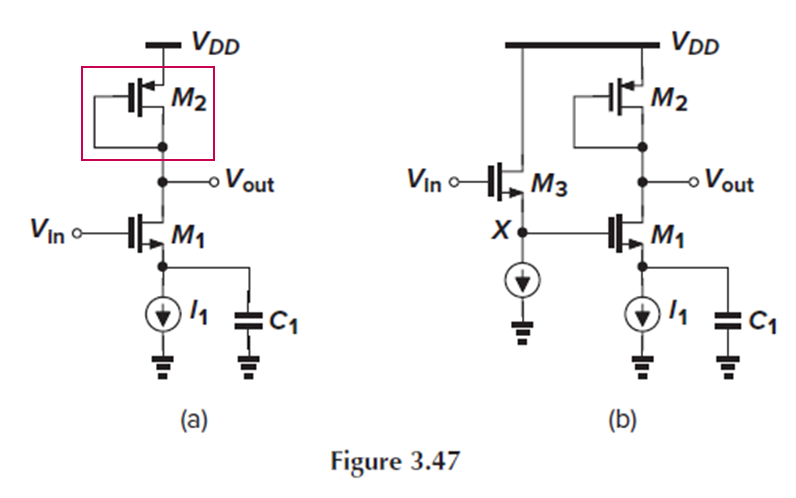
이 Example을 통해 source follower의 voltage-level shift 기능을 살펴봅시다.

<Solution>
(a) Fig. 3.47(a)는 M1의 source가 gnd에 연결되어 있고, gate에 Vin이 인가되는 CS stage이기 때문에, gain을 (3.101)처럼 –gmR2 형태로 나타낼 수 있습니다.
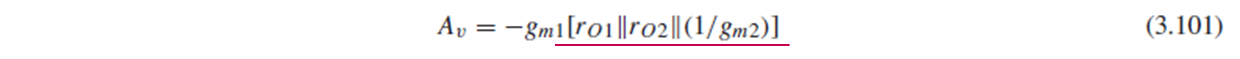
Vout = Vdd-|Vgs2|이므로, M1이 saturation이도록 하는 input 신호의 최대 dc level은 Vdd-|Vgs2|+Vth1입니다.
(b) Vin = Vdd라면, Vx = Vdd-Vds3 = Vdd-Vgs3입니다. Vin = Vdd일 때 M1이 saturation이려면, Vdd-Vgs3-Vth1 ≤ Vdd-|Vgs2|여야 하고, 따라서 Vgs3+Vth1 ≥ |Vgs2|여야 합니다.
'CMOS IC Design' 카테고리의 다른 글
| Cascode Stage, Folded Cascode [Razavi][Ch3] (0) | 2024.11.13 |
|---|---|
| CG Stage(Common-Gate Stage) [Razavi][Ch3] (5) | 2024.11.05 |
| CS Stage(6) - Source Degeneration [Razavi][Ch3] (0) | 2024.11.05 |
| CS Stage(5) - Triode Load [Razavi][Ch3] (0) | 2024.11.05 |
| CS Stage(4) - Active Load [Razavi][Ch3] (1) | 2024.11.05 |



