출처: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 3 - Single-Stage Amplifiers (pg. 75~82)
3.5. Common-Gate Stage
Common-Gate Stage
이전에 살펴본 CS stage와 source follower는 input 신호를 MOSFET의 gate로 인가했습니다.
그런데 common gate stage의 경우에는 source에 input 신호를 인가하고, drain에서 output을 생성합니다.
MOSFET의 gate는 원하는 동작에 맞게 dc voltage로 biasing합니다.

Fig. 3.48(a)의 회로를 보면, M1의 Id가 input signal source로 들어가고 있습니다.
달리 말하면, Fig. 3.48(b)에서 보듯, input 신호의 AC 성분만 capacitor C1을 통해 회로에 전달되고, M1의 gate에 필요한 Vb는 별도의 current source I1에 의해 설정되고 있습니다.
이를 두고 input 신호가 회로에 capacitively coupling되었다고 합니다.
Capacitively coupled input의 장점은, input의 DC 성분이 회로에 영향을 미치지 않고, 원하는 DC bias를 독립적으로 설정할 수 있다는 점입니다.
*Capacitive coupling: 커패시터를 사용하여 두 회로 간에 신호를 전달하는 방법입니다. 이때 커패시터는 직류(DC) 성분을 차단하고, 교류(AC) 성분만 전달하는 역할을 합니다. 즉, 입력 신호의 DC 성분은 전달되지 않고, 오직 AC 성분(변동하는 신호)만 회로로 전달됩니다.
CG Stage - Large Signal Behavior


Fig. 3.48(a)의 CG stage의 large-signal behavior를 살펴봅시다.
Channel-length modulation은 무시합니다.
M1이 켜지는 조건은 Vb-Vin ≥ Vth(Vin ≤ Vb-Vth)이고, saturation 되려면 Vout-Vin ≥ (Vb-Vin)-Vth(Vout ≥ Vb-Vth)를 추가로 만족해야 합니다.
즉, Vin ≤ Vb-Vth ≤ Vout 이면 M1이 saturation입니다.
Fig. 3.49의 그래프를 설명하겠습니다.
Vin이 큰 값에서부터 감소한다고 생각해 봅시다.
Vin ≥ Vb-Vth이면, M1이 off 상태이고, Id1=0이니 Rd를 통한 전압 강하가 없어서 Vout = Vdd입니다.
Vin ≤ Vb-Vth에 진입하면 M1이 켜져 Id1이 흐르면서, Vout이 Vdd보다 감소합니다.
Vout ≥ Vb-Vth까지는 saturation region이며, Id1 식은 (3.102)와 같습니다.

Vin이 더 감소하면 M1의 Vgs=Vb-Vin이 증가하여 Id1이 증가하고, Rd를 통한 전압강하가 증가하므로 Vout도 감소하게 됩니다.
Vout ≤ Vb-Vth부터는 triode region이고, (3.103)은 triode region이 시작되는 경계 조건인 Vout = Vdd-IdRd = Vb-Vth를 나타냅니다.

CG Stage - Small-Signal Gain
CG stage의 small-signal gain을 구해보겠습니다.
M1이 saturation에 있을 때 Vout 식을 (3.104)로 쓸 수 있습니다.

Small-signal gain을 구하기 위해 양변을 Vin으로 편미분하면 (3.105)가 됩니다.

그리고 Vin=Vsb임을 이용해 𝜂(에타)를 포함한 식으로 정리하면 small-signal gain을 (3.107)처럼 구할 수 있습니다.

CG stage의 gain은 양수죠.
CS stage와 source follower(CD stage)에서는 body effect를 나타내는 gmb나 𝜂가 gain의 분모에 들어가서 body effect가 gain을 감소시키는 효과가 나타났었습니다.
그런데 CG stage에서는 반대로, body effect가 stage의 effective gm을 증가시켜서 gain을 증가시킵니다.
CG Stage - Input Impedance (w/o Channel-Length Modulation)
CG stage의 input impedance를 구해봅시다.
Channel-length modulation은 무시합니다.

CG stage의 input impedance는 Fig. 3.48(a)의 CG stage M1의 source에서 본 impedance이자, Fig. 3.39(a)의 source follower의 output impedance와도 같습니다.
즉, CG stage의 input impedance는 source follower의 output impedance 1/(gm+gmb)와 같습니다.
따라서, body effect가 CG stage의 input impedance를 감소시킨다는 것을 알 수 있습니다.
CG stage가 비교적 낮은 input impedance를 가진다는 점이 유용하게 사용되는 경우가 있다고 합니다.
Example 3.17
이 example의 요지는, CS stage인 M1의 output에 CG stage를 연결했을 때 더 큰 gain을 얻을 수 있다는 것입니다.

두 Fig. 3.50(a)와 (b)의 gain 공식은 –gm1Rd로 같지만, CG stage를 연결한 (b)에서 Rd 값을 더 크게 설정할 수 있어 더 큰 gain을 얻을 수 있습니다.
<회로 설명>
Fig. 3.50에서, M1이 ΔV를 감지해서, 50Ω짜리 transmission line에 전류 Id가 흐르도록 하고 있습니다.
Fig. 3.50(a)에서는 transmission line의 다른 쪽에 50Ω 저항이 연결되어 있고, Fig. 3.50(b)에서는 저항 대신 CG stage가 달려 있습니다.
<문제 1>
첫 번째 문제는 저주파에서 두 회로의 Vout/Vin을 구하는 것입니다.
M1의 input이 ΔV만큼 변하면, M1의 drain current는 gm1ΔV만큼 변하고, 이 전류가 Rd에도 흐르므로 output voltage swing은 –gm1ΔVRd입니다.
두 회로에 대해 small-signal model을 그려보면, 두 회로 모두 Vout/Vin = -gm1Rd임을 알 수 있습니다.

<문제 2>
두 번째 문제는 node X에서 wave reflection을 최소화하기 위한 조건을 찾는 것입니다.
Transmission line의 반사 계수는 이 식과 같이 정의됩니다.

ZL은 transmission line 끝에서 본 load impedance, Z0은 transmission line에서 본 characteristic impedance로, 고주파 신호 전송에서 characteristic impedance Z0는 50Ω을 표준으로 하고 있습니다.
X에서의 wave reflection을 최소화하기 위해서는, 반사 계수가 0, 즉, ZL = Z0 = 50Ω이 되어야 합니다.
이를 impedance matching이라고 합니다.
Fig. 3.50(a)에서 ZL은 Rd니까, transmission line의 반사를 최소화하려면 Rd=50Ω이어야 합니다.
Fig. 3.50(b)에서 ZL은 M2의 source에서 본 resistance로, 이 값이 50Ω이 되면 X에서의 반사는 최소화됩니다.
여기서 주목해야 할 점은, 이 경우에 Rd 값은 impedance matching과 상관이 없다는 점입니다.
따라서 CS stage의 Rd=50Ω이어야 하는 (a) 경우보다, (b)에서는 Rd를 50Ω보다 크게 만들 수 있기 때문에 더 큰 gain을 얻을 수 있는 것입니다.
CG Stage - Rs Added
이번엔 CG stage의 좀더 general한 case를 살펴보겠습니다.

Fig. 3.51(a) 회로가 이전에 봤던 CG stage와 다른 점은, M1의 source 단에 Rs가 달려 있다는 점입니다.
Fig. 3.51(a)의 회로는 Fig. 3.51(b)의 small-signal circuit으로 나타낼 수 있습니다.
회로에서 KVL을 적용한 (3.108)을 V1에 대한 식으로 나타내고 (3.109)애 대입해서 (3.110)을 얻을 수 있습니다.
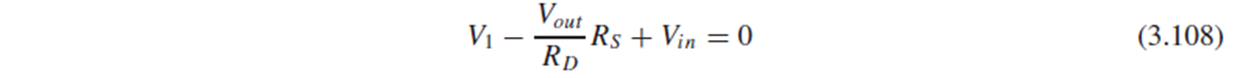


이걸 정리하면 이 회로의 gain은 (3.111)이 됩니다.

Example 3.18
이 example은 CS stage의 load로 CG stage가 사용된 회로의 gain을 구하는 문제입니다.
Channel-length modulation과 body effect를 둘다 고려합니다.

CS stage transistor가 M1, CG stage의 transistor가 M2입니다.
CS stage 부분의 thevenin equivalent 회로를 그리면 Fig. 3.52(b)가 됩니다.
이때 Vin,eq(3.112)와 Req(3.113)를 구해 overall gain을 (3.114)처럼 구할 수 있습니다.



CG Stage - Input Impedance
아까는 channel length modulation은 없고, body effect만 있는 특수한 경우의 CG stage input impedance를 1/(gm+gmb)로 구했습니다.
이번에는 channel-length modulation까지 고려해서 CG stage의 input impedance를 구해보겠습니다.

Fig. 3.53(a)의 small-signal equivalent circuit을 Fig. 3.35(b)로 그렸습니다.
여기서 V1 = -Vx이고, ro에 흐르는 전류는 KCL에 의해 아래와 같습니다.

(3.115)와 같이 KVL 식을 쓰고, Vx/Ix 식을 정리하면 input impedance가 (3.117)으로 구해집니다.


Source에서 본 drain impedance Rd가 (gm+gmb)ro만큼 감소한다는 것을 알 수 있습니다.
즉, CG stage의 input impedance가 매우 낮아져서, input 신호를 효율적으로 전달할 수 있습니다.

그런데 short-channel device에서는 intrinsic gain인 gmro가 작기 때문에, input impedance가 충분히 작지 않아, input 신호가 효율적으로 전달되지 못하는 문제가 발생합니다.
여기서 두 가지 특수한 case를 살펴보겠습니다.
첫째, Rd=0인 case입니다.


여기서 Rd=0이면 input impedance가 (3.118), (3.119)가 됩니다.

그런데 이는 source follower의 source에서 본 output resistance와 같습니다. (Fig. 3.39) (Source follower에서도 channel-length modulation을 고려하면)
Rd=0인 CG stage와 Fig. 3.39(a)가 서로 같으니까 당연한 결과입니다.

둘째, Rd를 ideal한 current source로 대체하는 경우입니다.
그러면 Rd=∞가 되므로, (3.117)에 의해 input impedance도 ∞가 됩니다.
이를 Fig. 3.54로 설명해 보겠습니다.
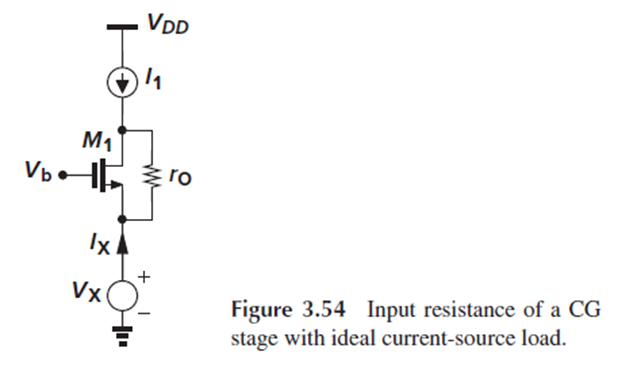
M1에 흐르는 총 전류가 I1로 고정이므로, Vs의 변화가 M1에 흐르는 전류는 변화시킬 수 없어, Ix=0가 되어 Vx/Ix=∞가 되는 것이죠.
즉, CG stage의 drain에 연결된 load impedance가 작을 때만 input impedance도 작은 값일 수 있다는 것이 요지입니다.
(Example 3.19) 이어서, load가 current source인 CG stage의 voltage gain을 구해보겠습니다.
CG stage의 load가 current source이면 load resistance Rd가 ∞입니다.
이전에 구했던 (3.111)에 Rd=∞를 대입하면, (3.120)이 됩니다.


여기서 주목할 만한 점은, gain이 Rs에 의존하지 않는다는 겁니다.
직전 슬라이드에서 Rd=∞이면 M1의 source에서 본 input impedance도 ∞라는 결론이 나왔었죠.
Source에서 본 input impedance가 ∞라는 건 source를 통해 들어가는 전류가 0이라는 거니까, Rs를 통한 전압 강하가 없다는 겁니다.
그래서 Vin이 그대로 Vx에 전달될 수 있고, Fig. 3.55(b)처럼 Rs는 없는 것이나 마찬가지가 됩니다.

CG Stage - Output Impedance
CG stage의 output impedance를 구해보겠습니다.
그 전에 알아야 할 것이, CG stage의 drain에서 본 Rs는 CG stage의 gain인 [1+(gm+gmb)ro]만큼 증폭되어 보인다는 것입니다.
Source에서 본 Rd+ro는 1/[1+(gm+gmb)ro]배만큼 작게 보인다는 것도 알아둡시다.

이제 CG stage의 output impedance Rout을 구해 보면, Rout은 test voltage Vx가 인가된 branch 기준으로 위와 아래 저항의 병렬 연결일 것입니다.

위쪽 저항은 Rd이고, 아래쪽 저항은 ro와 증폭된 Rs의 직렬 연결인데, 위쪽과 아래쪽 저항의 병렬 연결이 Rout입니다.

CG Stage - Input Signal as a Current
(Example 3.20)

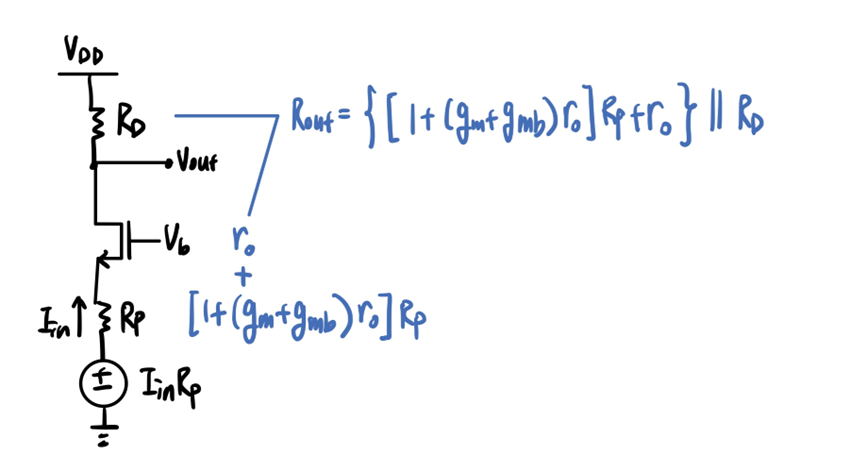
CG stage의 input 신호가 전압이 아니라 전류라면 Rout은 어떻게 될까요? (Fig. 3.58)
Vout/Iin을 구하기 위해 thevenin equivalent를 사용하면 그림과 같고, Rout을 (3.123)으로 쉽게 구할 수 있습니다.

'CMOS IC Design' 카테고리의 다른 글
| PVT(Process, Voltage, Temperature) Variation (1) | 2024.11.13 |
|---|---|
| Cascode Stage, Folded Cascode [Razavi][Ch3] (0) | 2024.11.13 |
| Source Follower(CD Stage) [Razavi][Ch3] (1) | 2024.11.05 |
| CS Stage(6) - Source Degeneration [Razavi][Ch3] (0) | 2024.11.05 |
| CS Stage(5) - Triode Load [Razavi][Ch3] (0) | 2024.11.05 |



