참고: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 3 - Single-Stage Amplifiers (pg. 47~52)
2024.10.29 - [CMOS IC Design] - (개요) Single-Stage Amplifiers [Razavi][Ch3]
(개요) Single-Stage Amplifiers [Razavi][Ch3]
참고: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second EditionChapter 3 - Single-Stage Amplifiers (pg. 45~47)3.1. ApplicationsAmplifier는 휴대폰, 노트북, 디지털 카메라 등의 전자기기에 모두 쓰입니다. 전자기기
soobdal.tistory.com
<목차>
Common-Source Stage with Resistive Load
Vout-Vin Graph
CS Stage Gain
CS Stage MOSFET의 Id, gm
Voltage Gain of CS Stage (Example 3.1)
CS Stage w/ Sinusoid Input (Example 3.2)
Maximizing Voltage Gain of CS Stage
CS Stage w/ Channel-Length Modulation
Current Source Load - Voltage Gain and Load Impedance
Vin in MOSFET Bulk (Example 3.4)
Overview: Diode-Connected Load
3.3. Common Source Stage
3.3.1. Common-Source Stage with Resistive Load
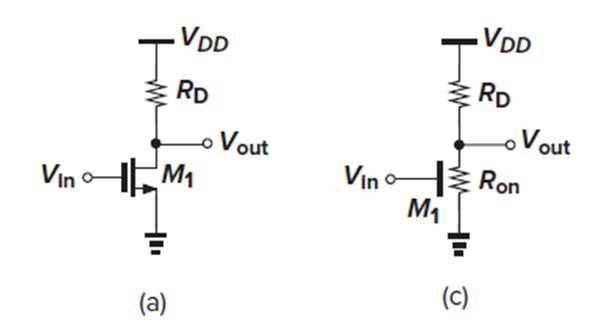
Common-Source Stage with Resistive Load

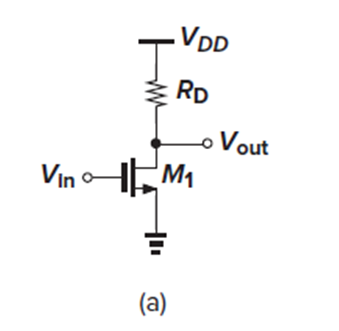
Common source amp는 Fig. 3.4(a) 그림처럼 G가 input, D가 output인 amp입니다.
Vin, 즉 Vgs가 0일 때는 NMOS M1이 off니까 Id = 0이고, Rd를 통한 전압 강하가 없으니까 Vout = VDD겠죠.
그러다가 Vin이 Vth가 되면 M1이 켜지면서 Rd를 통한 전압 강하가 발생해서 Vout이 점점 감소합니다.
Channel-length modulation을 고려하지 않는다면 Vout 식은 (3.3)과 같습니다.

Vin이 계속 증가하다가 Vout보다 Vth만큼 커지면, 즉 Vout = Vin – Vth이면(3.4), Vin – Vth, 즉 Vout을 구할 수 있습니다.

이 지점은 Fig. 3.4(b)의 A와 같고 이때의 Vin을 Vin1이라 하겠습니다.
Vin > Vin1이면, M1이 triode region에 있게 되어 Vout이 (3.5)로 나타내어집니다.

(Vin1 = Vout+Vth, Vin = Vgs, Vout = Vds 이므로 Vin > Vout+Vth à Vgs – Vth > Vds와 같은 의미이기 때문입니다.)
Vout-Vin Graph

Vin이 엄청 커져서 M1이 deep triode region에 진입한다면, 즉, Vout << 2(Vin – Vth)이라면, 트랜지스터가 Vgs 값에 의해 조절되는 저항과 같이 동작합니다. (Fig. 3.4(c))
그 저항값은 (2.11)과 같고, 이를 (3.6)에 대입하면 Vout의 식은 (3.7)과 같이 나타납니다.



CS Stage Gain
CS stage의 gain을 구해봅시다.
Gain은 Vout을 Vin으로 편미분한 값이고, Vout 식으로 (3.3)을 사용하면 CS stage의 gain은 -gmRd가 됩니다.
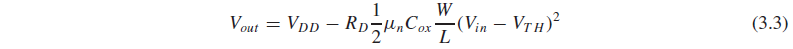
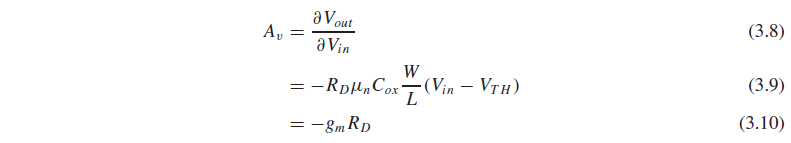
이는 직관적으로도 생각해볼 수 있는데, input 전압이 ΔVin만큼 바뀌면 Id가 gmΔVin만큼 바뀌어서, output 전압이 -gmRdΔVin만큼 바뀌겠죠.
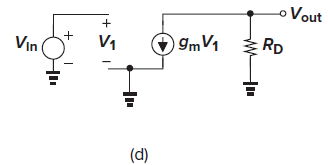
Fig. 3.4(d)의 small-signal model에서 Vout = - gmV1Rd = - gmVinRd 라고 생각할 수도 있습니다.
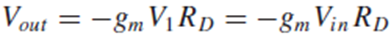
회로의 signal swing이 크다면 Av = -gmRd에서 gm이 영향을 받아 amp의 gain이 달라질 수 있습니다.
gm은 아래 수식과 같으므로 Vgs = Vin에 따라 gain이 변해버립니다.
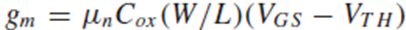
Amp의 동작이 nonlinear하다는 거죠.
이 nonlinearity를 감소시키기 위해서는 gain이 gm같은 signal-dependent parameter의 영향을 적게 받아야 합니다.
CS Stage MOSFET의 Id, gm
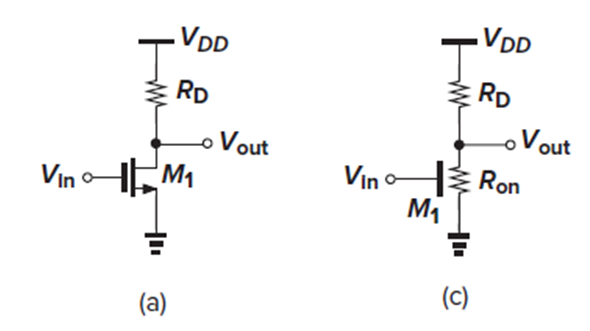
Fig. 3.4(a)의 회로에서, M1의 Id와 gm을 구해보겠습니다.
먼저 Id를 보면, M1의 Vin > Vth일 때부터 Id가 유의미한 값을 가지게 됩니다.
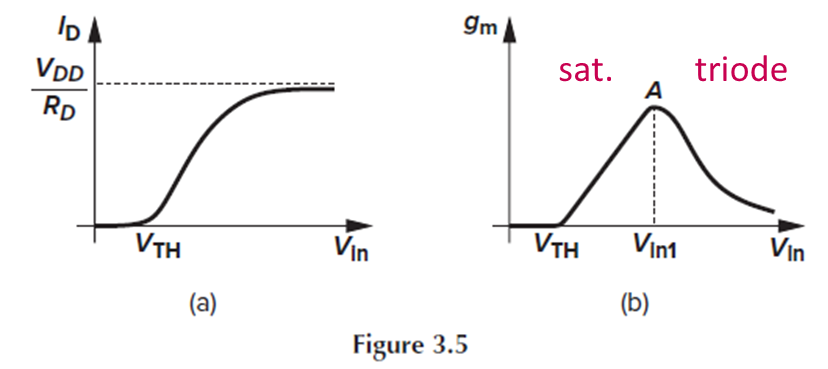
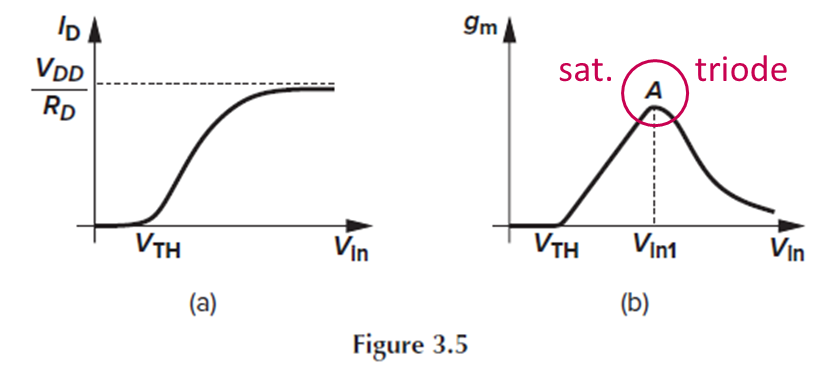
Fig. 3.5(a) 그래프에서 Vin=Vth 부근부터 Id가 증가하기 시작하죠.
Ron<<Rd일 때, Vdd=Id(Rd+Ron)≈IdRd가 되므로, Vin이 Vth를 넘어 계속 증가할 때 Id는 Vdd/Rd에 가까워집니다.
이제 M1의 gm을 구해보겠습니다.
Saturation region에서의 gm의 식을 보면, Vin > Vth에서 gm이 증가하기 시작합니다.
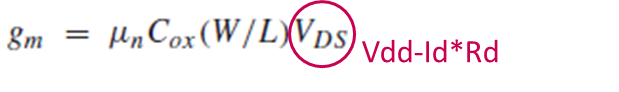
Triode region에서는 gm이 Vds에 대해 linear한데요. 이 식만 봐서는 gm과 Vin의 관계가 나타나지 않습니다.
Vds = Vout = Vdd-Id*Rd인데 triode region에서의 Id가 (2.8)과 같고, (2.8)의 Vgs가 Vin이죠.
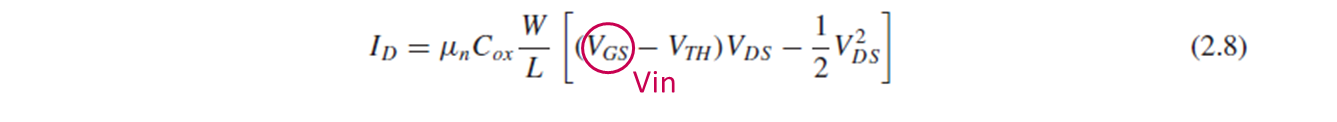
이 두 식을 연립하면 gm과 Vin의 관계를 알아낼 수 있습니다.
Voltage Gain of CS Stage (Example 3.1)
앞에서 봤던 triode에서의 Vout 수식 (3.5)로부터 이 amp의 gain도 구할 수 있습니다. (3.11)
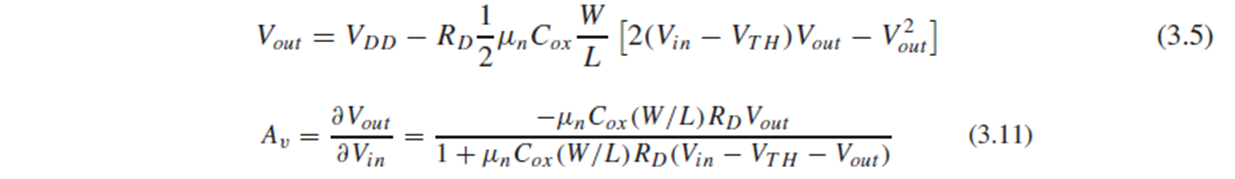
이는 Vout = Vin-Vth일 때 최대값을 가지고, Fig. 3.5(b)의 피크 지점 A에 해당합니다.
CS Stage w/ Sinusoid Input (Example 3.2)
CS stage의 input이 sinusoid로 주어질 때 트랜지스터 M1의 gm을 시간의 함수로 구해봅시다.
Vin은 아래와 같이 주어지고, V0는 bias, V1은 트랜지스터를 off와 triode로 drive할 수 있을 정도로 큰 값입니다.
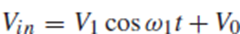
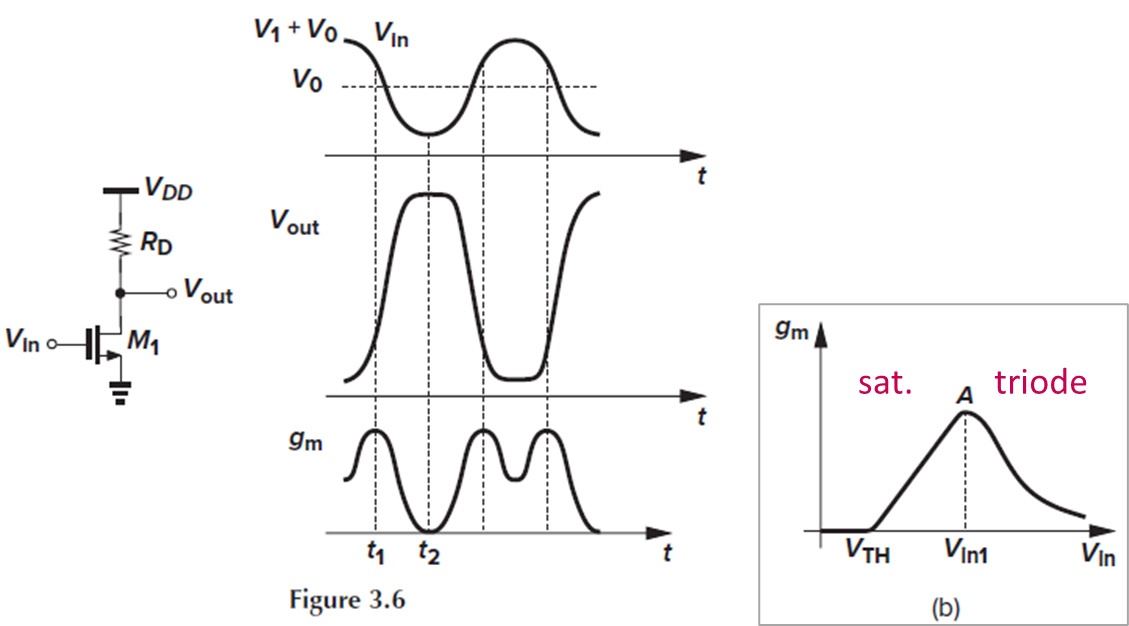
만약 Vin = V1+V0일 때, 즉 input이 최대일 때, Vout은 Rd의 전압강하로 인해 작은 값일 것이고, M1은 triode region에 있을 것이고(Vout < Vin-Vth일 테니), gm은 작은 값일 것입니다(왜?).
2) 0 < t ≤ t1
Vin이 작아지면 Id*Rd가 감소하면서 Vout이 증가할 것이고, gm이 증가하다가 최대가 되는 t=t1에서 M1이 saturation에 진입할 것입니다. (Fig. 3.5(b) 참고)
t=t1인 지점은 앞에서도 다뤘듯 Vin-Vout = Vth인 지점입니다.
3) t1 < t ≤ t2
Vin이 더 작아지면 Id 감소, Vout 증가가 계속되고, gm은 피크 이후 감소합니다.
그러다가 Vin이 최소값인 t=t2에서 Vout=0, gm=0이 됩니다.
Maximizing Voltage Gain of CS Stage
CS stage의 voltage gain은 (3.10)에서 구했듯 Av = -gmRd이고, 이를 (3.12)와 (3.13)과 같이 나타낼 수 있습니다.
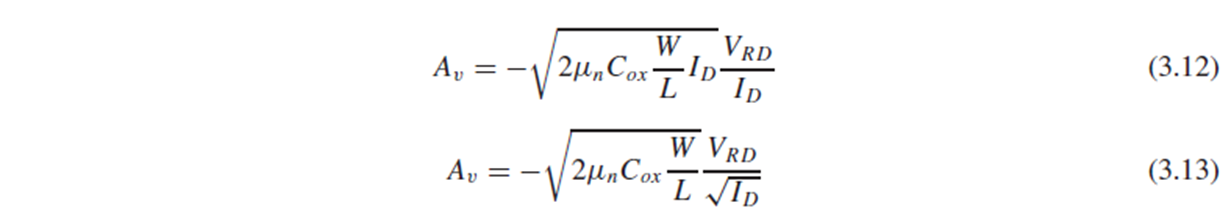
(3.13)에 의하면 W/L이나 Vrd(Rd 양단의 전압)를 늘리거나 Id를 줄이면 gain을 증가시킬 수 있습니다.
Device 크기가 커지면 capacitance도 늘어나고, Vrd가 늘어나면 최대 voltage swing을 제한하게 됩니다.
예를 들어, M1의 Vds = Vdd-Vrd = Vin-Vth이면, M1은 triode region의 경계에 있습니다.
따라서 input과 output에서 아주 작은 swing만 가능합니다.
만약 Vrd를 일정하게 유지하고 싶은데 Id가 감소하면, Rd가 증가해야 합니다.
그러면 output node의 time constant가 증가하게 됩니다.
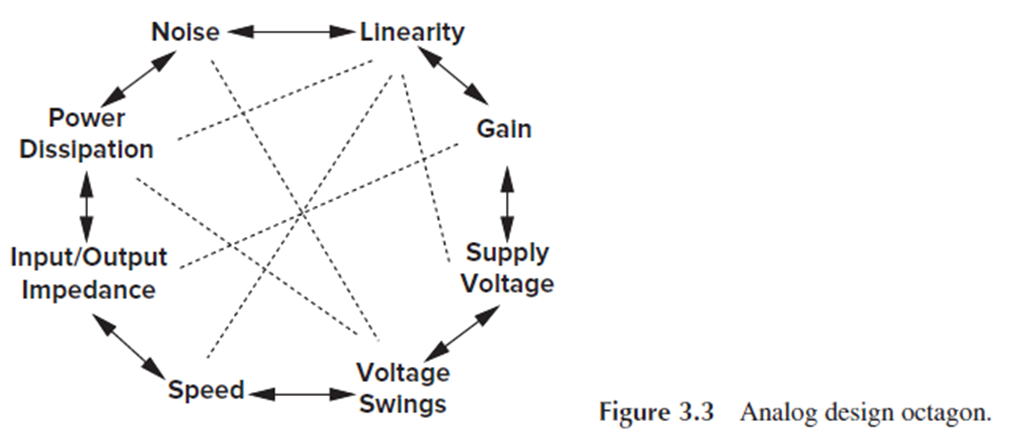
달리 말하면, analog design octagon에서 볼 수 있듯 gain, bandwidth, voltage swing에서 tradeoff가 발생합니다.
Supply voltage가 작으면 이 tradeoff가 강해집니다.
CS Stage w/ Channel-Length Modulation
Rd가 커지면, M1의 channel-length modulation 효과가 커집니다.
Channel-length modulation은 Vds에 따라 Id가 변하는 효과였죠.
Rd가 커지면 output swing이 커지면서 M1의 Vds 변화폭이 커지고, Vds의 변화폭이 커지면 Id 변화가 커져, channel-length modulation이 뚜렷해진다고 할 수 있습니다.
(3.3)의 수식에 channel-length modulation을 추가하면 (3.14)가 됩니다.
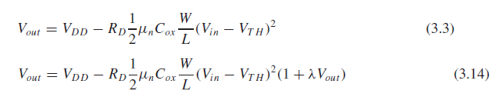
(3.14)로부터 gain을 구하기 위해 Vout을 Vin으로 편미분하면 (3.15)와 같이 됩니다.
여기서 긴 항을 1/ro로 치환하여 gain 식을 정리하면 (3.17)이 됩니다.
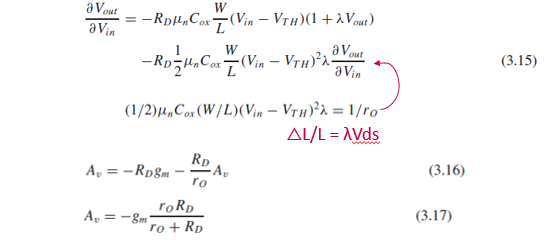
Small-signal model로 확인한 gain도 같은 값이 나옵니다.

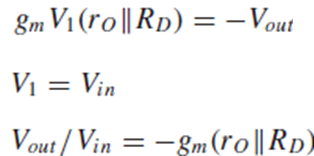
Current Source Load - Voltage Gain and Load Impedance
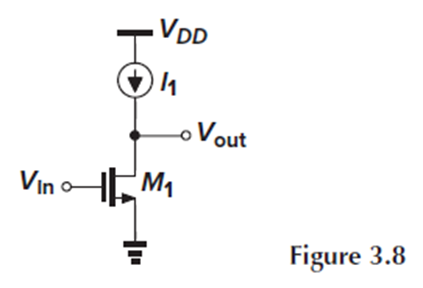
M1이 saturation에서 동작할 때, small-signal voltage gain을 구해 봅시다.
I1은 전류원으로, 이상적으로 출력 임피던스가 무한대여야 외부 조건의 영향을 받지 않고 일정한 전류를 공급할 수 있습니다.
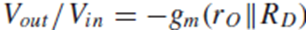
Rd=∞이므로, gain은 M1의 ro에 의해 정해지게 됩니다.
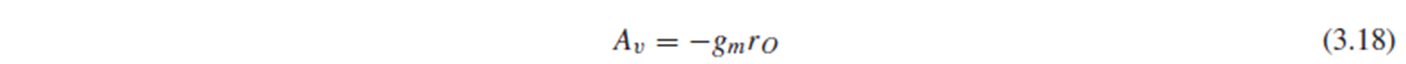
gmro 값을 트랜지스터의 “intrinsic gain”이라고 하는데, 이는 한 device로 얻을 수 있는 최대 voltage gain을 나타냅니다.
오늘날 CMOS 기술에서 short-channel device의 gmro 값은 대략 5에서 10 사이입니다.
보통 1/gm << ro를 가정합니다.
이 회로에서는 I1이 current source로 일정하고, KCL에 의해 M1의 drain current Id1이 I1과 같아야 합니다.
수식들을 보면, Id1=I1로 일정하려면 Vin과 Vout이 서로의 변화를 상쇄해야 합니다.
예를 들어, Vin이 증가하면 Vout이 감소하는 식이죠.
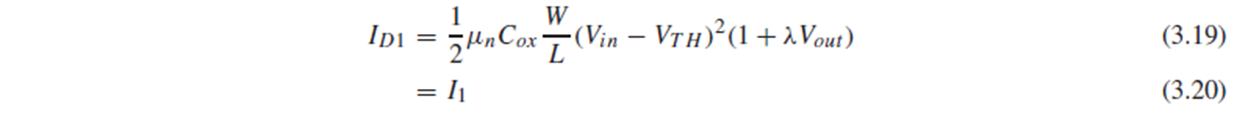
여기서 짚고 넘어가야 할 점은, voltage gain을 최대로 만들기 위해서는 load impedance가 최대가 되어야 한다는 것입니다.
– gmro가 – gm(ro||Rd)보다 무조건 크기 때문입니다. (ro-(ro||Rd)>0으로 증명 가능)
Vin in MOSFET Bulk (Example 3.4)
만약 Vin을 MOSFET의 bulk에 인가하면 어떻게 될까요?
Channel-length modulation은 없다고 가정합시다.
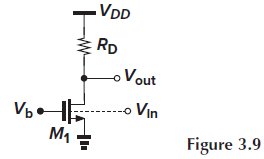
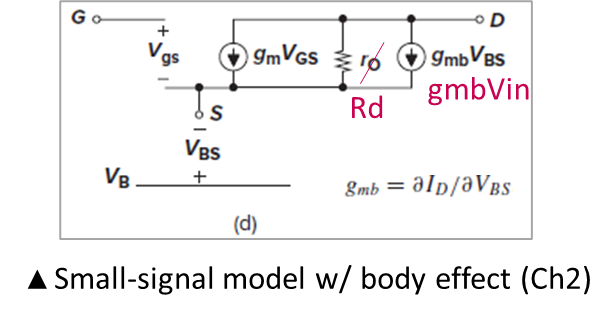
MOSFET bulk에 Vin을 가하면, bulk potential이 Vth에 영향을 미쳐 gate-source overdrive (Vgs - Vth)도 바꾸는 body effect가 발생합니다.
Ch2의 small-signal model 부분에서 봤듯, body effect가 있는 상황에서 Id = gmbVin입니다.
따라서 gain Av = - gmbRd입니다.
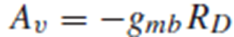
Overview: Diode-Connected Load
어떤 CMOS 기술에서는 저항값을 정확하게 만들거나 사이즈를 reasonable하게 만들기 어렵습니다.
따라서 Rd를 MOSFET으로 대체하는 것이 좋은데, 여기서 diode-connected load가 등장합니다.
Diode-connected load는 다음 포스팅에서 다뤄보도록 하겠습니다.
2024.10.29 - [CMOS IC Design] - CS Stage(2)-Diode-Connected Load [Razavi][Ch3]
CS Stage(2)-Diode-Connected Load [Razavi][Ch3]
출처: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second EditionChapter 3 - Single-Stage Amplifiers (pg. 52~58)3.3. Common Source Stage3.3.2. Common-Source Stage with Diode-Connected LoadCommon-Source Stage with Diode-Connected Load지난
soobdal.tistory.com
'CMOS IC Design' 카테고리의 다른 글
| CS Stage(3)-Current-Source Load [Razavi][Ch3] (1) | 2024.10.29 |
|---|---|
| CS Stage(2)-Diode-Connected Load [Razavi][Ch3] (1) | 2024.10.29 |
| (개요) Single-Stage Amplifiers [Razavi][Ch3] (0) | 2024.10.29 |
| FinFETs, MOSCAP [Razavi][Ch2] (0) | 2024.10.29 |
| Small-Signal Model [Razavi][Ch2] (1) | 2024.10.07 |



