출처: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 3 - Single-Stage Amplifiers (pg. 52~58)
3.3. Common Source Stage
3.3.2. Common-Source Stage with Diode-Connected Load
Common-Source Stage with Diode-Connected Load
지난 포스팅에서는 resistive load가 있는 common-source stage를 알아봤습니다.
그런데 어떤 CMOS 기술에서는 저항값을 정확하게 만들거나 사이즈를 reasonable하게 만들기 어렵습니다.
따라서 Rd를 MOSFET으로 대체하는 것이 좋습니다.
이걸 어떻게 하냐면, MOSFET의 G과 D를 연결하면(short시키면) small-signal resistor로 동작하는 점을 이용합니다.

“Diode-connected” device라고도 하는 이 구조는 two-terminal resistor와 같은 small-signal 특성을 갖습니다.
그리고 D와 G가 연결되어 있으니 Vd=Vg (Vds=Vgs)라서, Vds > Vgs – Vth를 항상 만족하여 항상 saturation에 있습니다.
이 diode의 small-signal model을 살펴보면, source에서 본 impedance가 1/gm으로 근사됩니다.
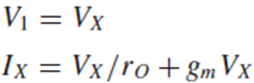

Body Effect 고려
만약 body effect를 고려한다면, Fig. 3.11의 small-signal circuit을 그릴 수 있습니다.
이러한 과정을 통해 source에서 본 impedance를 (3.22)로 구할 수 있고, ro가 매우 크므로 (3.24)로 근사할 수 있습니다.


General한 case에서는 impedance를 1/gm, ro, 1/gmb의 병렬저항값으로 나타냅니다.
Body effect를 고려했을 때 M1의 source에서 본 impedance가 더 작다는 것을 알 수 있습니다.
MOSFET Source에서 본 Impedance
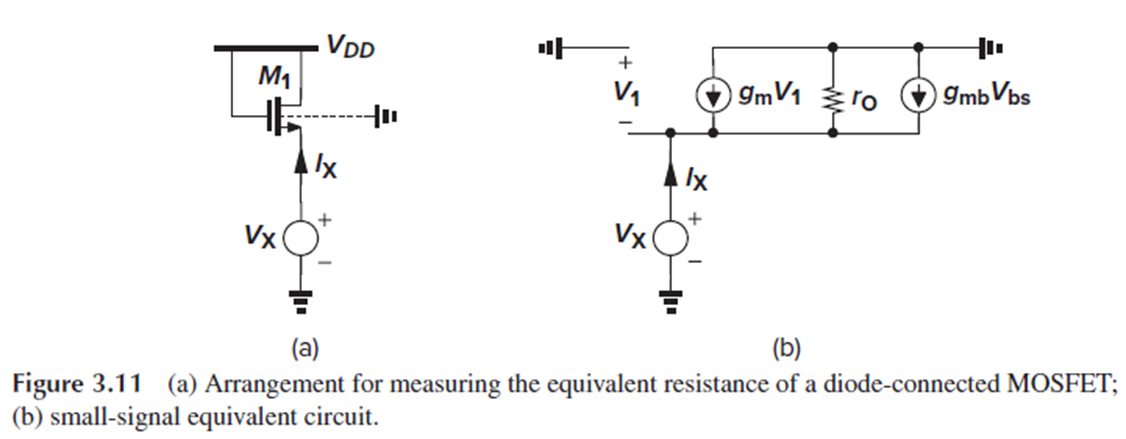
Diode-connected load가 없는 CS stage의 M1 source에서 본 impedance를 구해봅시다.
Small-signal model에 의해, impedance가 1/(gm+gmb)라는 결론이 나왔습니다.
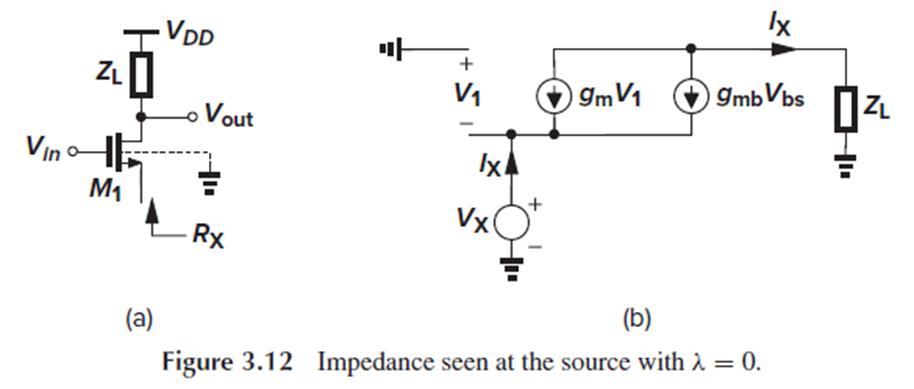
Fig. 3.12(b)에서 M1의 drain이 ac ground가 아니라는 것 빼고는 Fig. 3.11(a)와 Fig. 3.12(a)의 회로는 비슷합니다.

Fig. 3.11(a)의 회로에서 λ=0이라면, 두 회로의 MOSFET source에서 본 impedance는 같습니다.
Channel-length modulation과 body effect를 무시했을 때, 즉 λ=γ=0일 때, MOSFET의 source에서 본 impedance는 1/gm이라는 중요한 결론이 여기서 나옵니다.
Linearity of CS Stage w/ Diode-Connected Load
이제 본격적으로 diode-connected load가 있는 common-source stage를 분석해 봅시다.
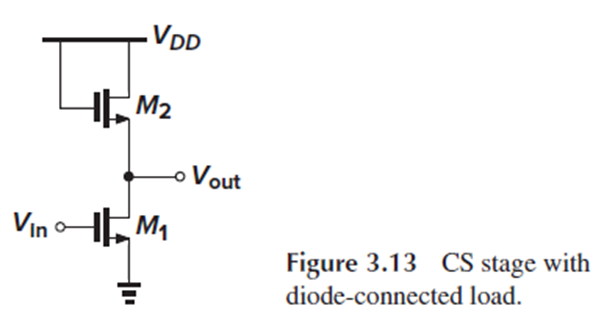
Channel-length modulation을 무시 가능할 때, body effect가 있을 때 source에서 본 impedance (3.24)를, resistive load가 있는 CS stage의 gain인 (3.10)에 대입하여 load impedance를 (3.28)과 같이 구할 수 있습니다.

(3.24)는 M2의 source에서 본 impedance, (3.10)은 M2를 load로 갖는 CS stage의 gain인 것이죠.
(2.19)의 gm 식을 대입하여 (3.29)를 얻고, Id1=Id2이므로 식을 (3.30)으로 축소할 수 있습니다.

이 식에서 알 수 있는 중요한 점은, M1이 saturation일 때, output voltage에 따른 η(eta, 에타)의 변화를 무시한다면, gain이 bias 전류와 전압에 무관하다는 점입니다.
다시 말해, input과 output 신호가 변해도 gain이 일정하게 유지됩니다.
이는 input-output 특성이 비교적 linear하다는 것을 의미합니다.
Linearity of CS Stage w/ Diode-Connected Load
Diode-connected load를 가진 CS stage의 linearity는 large-signal analysis로도 검증할 수 있습니다.
편의상 channel-length modulation을 무시하면, Fig. 3.13에서 M1과 M2에 흐르는 drain current가 같으므로 (3.31)과 (3.32)를 얻습니다.
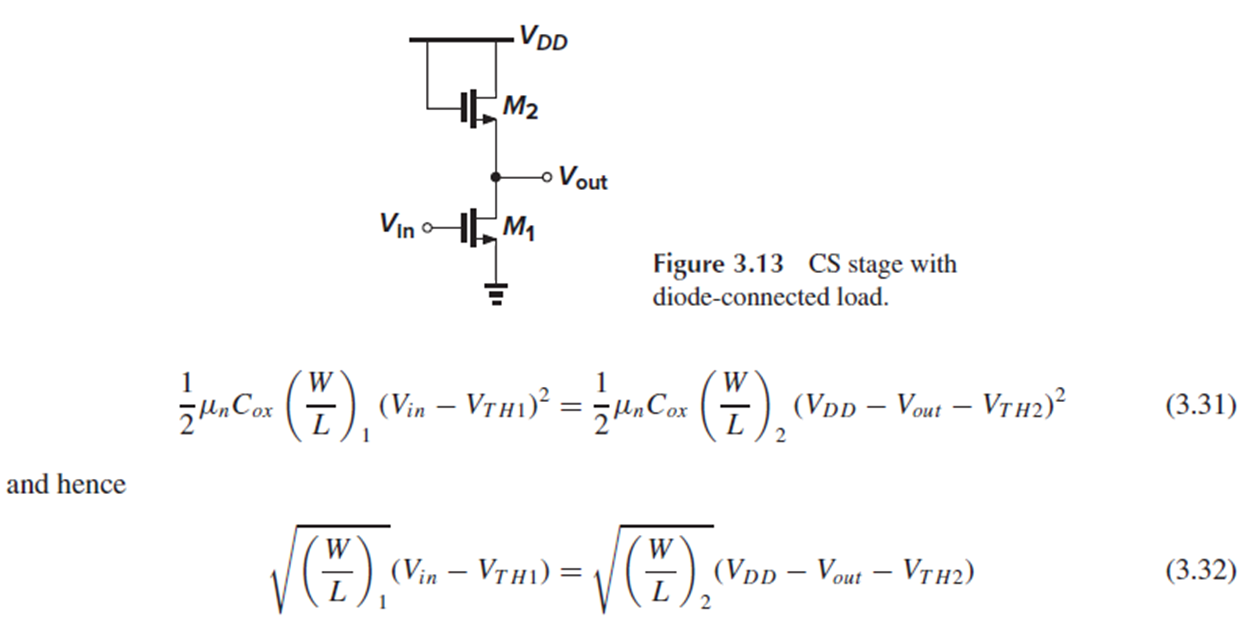
따라서, Vout에 따른 Vth2의 변화가 작다면, 이 회로의 input-output 특성이 linear하다고 할 수 있습니다.
이 회로의 양변을 Vin으로 미분해서 chain rule을 적용하면 앞 슬라이드의 gain 식과 같은 식을 얻을 수 있는데, 이 부분은 수학이라 생략하겠습니다.
Output Capacitance

Fig. 3.14(a)의 회로에서 I1=0으로 떨어질 때 Vout은 어떻게 변할지 살펴봅시다.
이 case를 분석하는 이유는, 곧이어 Fig. 3.13 회로의 input-output characteristic을 분석할 때 Vin<Vth case, 즉 Id1=0일 때의 Vout을 알아보기 위함입니다.
I1이 곧 M2의 drain current나 마찬가지니까, I1이 감소하다는 것은 M2의 Vgs가 감소한다는 것이죠.
M2의 Vov = Vgs-Vth가 감소하게 됩니다.
따라서 작은 I1에 대해 Vgs2 ≈ Vth2, Vout = Vdd-Vds = Vdd-Vgs ≈ Vdd-Vth2입니다.
그런데, Id가 0에 가까워질 때 M2의 subthreshold conduction이 결국에는 Vout을 Vdd와 가까운 값으로 만들기는 하지만, 그러기까지 시간이 조금 걸립니다.
Output node에 있는 capacitance에 의해 Vout = Vdd-Vth2에서 Vout=Vdd로 변하기까지 시간이 걸리는 것입니다. (Fig. 3.14(b))
그렇기 때문에 switching이 잦은 회로에서는 I1이 0에 가까워질 때 Vout이 Vdd-Vth2 근처에서 움직일 것이라 추측할 수 있습니다.
Input-Output Characteristic

다시 Fig. 3.13의 diode-connected load가 있는 CS stage를 보고, input-output characteristic을 따져 봅시다.
Vin < Vth1일 때는 M1이 OFF라 Id1이 0에 가깝고, 앞서 살펴본 대로 Vout = Vdd-Vth2입니다.
Vin > Vth1이 되면 Vout이 (3.32)에서 살펴본 대로 거의 직선 그래프를 그립니다.

Vin이 Vout+Vth1을 넘으면, 즉 A 지점을 넘으면, M1이 triode region에 진입하면서 nonlinear한 특성을 띠게 됩니다.
CS Stage w/ Diode-Connected PMOS Device


Body effect와 channel-length modulation을 무시한다면, PMOS diode가 연결된 CS stage의 gain은 (3.35)로, NMOS case와 비슷합니다.
높은 Gain을 얻는 방법


결론적으로, diode-connected load가 연결된 CS stage는 NMOS를 쓰든 PMOS를 쓰든, device dimension에 그리 큰 영향을 받지 않습니다.
높은 gain을 위해서는 input device의 W/L은 크게, load device의 W/L은 작게 설계해야 합니다.
W/L이 gain에 끼치는 영향에 대한 수치적 감을 잡을 수 있는 예시가 아래에 나와있습니다.

Tradeoff between Gain and Voltage Swings
Diode-connected load가 연결된 CS stage의 경우, Gain과 voltage swing 간의 tradeoff가 발생합니다.
그말인즉슨, 높은 gain을 얻으려다 보면 voltage swing이 감소하게 된다는 것입니다.

Fig. 3.16 회로에서 Id1 = |Id2|인 것을 (3.36)과 같이 쓸 수 있고, channel-length modulation을 무시하면 (3.37)을 얻습니다.


아까처럼 gain=5의 높은 gain을 얻기 위해서는, Vgs1-Vth1 = 100mV이고 |Vth2| = 0.3V인 상황에서 Vgs2가 0.8V나 되어야 합니다.
이렇게 되면 output swing이 심각하게 줄어들게 됩니다.
Load에 Current Source 추가
M1이 saturation에서 동작하고, channel-length modulation을 무시할 때, Is = 0.75*I1을 추가한 case에서 (3.37)이 어떻게 변하는지 살펴보겠습니다.

|Id2| = I1/4이므로, (3.27)~(3.30)을 참고하여 gain은 (3.41)과 같이 나타낼 수 있습니다.

또한, |Id2| = I1/4를 식으로 나타내면 (3.42)가 되어, (3.43)의 관계를 얻을 수 있습니다.

이 Example에서 말하고 싶은 건, gain 5을 얻기 위해서는 M2의 overdrive가 M1 overdrive의 1.25배만 되면 된다는 것입니다.
달리 말하면, Is를 추가함으로써 4배의 gain을 얻을 수 있습니다.
Overview: Current-Source Load
바로 위의 example에서 봤듯이, load에 current source를 추가하면
높은 gain을 얻을 수 있습니다.다음 포스팅에서는 current-source load를 가진 CS stage에 대해 알아보겠습니다.
'CMOS IC Design' 카테고리의 다른 글
| CS Stage(4) - Active Load [Razavi][Ch3] (1) | 2024.11.05 |
|---|---|
| CS Stage(3)-Current-Source Load [Razavi][Ch3] (0) | 2024.10.29 |
| CS Stage(1) - Resistive Load [Razavi][Ch3] (0) | 2024.10.29 |
| (개요) Single-Stage Amplifiers [Razavi][Ch3] (0) | 2024.10.29 |
| FinFETs, MOSCAP [Razavi][Ch2] (0) | 2024.10.29 |



