참고: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 5 - Current Mirrors and Biasing Techniques (pg. 146~160)
5. Current Mirrors and Biasing Techniques
5.3. Active Current Mirrors
5.3 단원은 OTA라고 하는 “operational transconductance amplifier”에 대한 내용입니다.
OTA는 current mirror를 load로 가지는 differential pair입니다.

Fig. 5.22의 M3와 M4가 current mirror입니다.
M3의 bias가 고정된 전압이 아니라, M1의 drain에 연결되어 있습니다.
따라서 current mirror에 흐르는 전류가 Vin에 dependent해서, 이를 active current mirror라고 합니다.
OTA를 알아보기 전에, passive load를 가진 differential pair부터 보고 왜 active load가 필요한지 알아보겠습니다.
OTA의 Small-Signal Gain 구하기 - 방법 (1)

Fig. 5.23(a)는 passive load를 가진 differential pair입니다.
OTA에서의 active load와 달리, M3에 흐르는 전류가 I1으로 고정되어 있죠.
두 가지 방법으로 이 회로의 small-signal gain을 구해 보겠습니다.
이 회로의 small-signal gain은 Av = Vout/Vin = GmRout입니다.
i) Gm 구하기
Fig. 5.23(b)처럼 Gm 계산을 위해 output이 ac gnd로 short되면, M1과 M2는 서로 대칭적이게 됩니다.
즉, gm1과 gm2가 같아집니다.

Differential pair가 single-ended이므로 Iout=1/2*(id1-id2)입니다.
따라서 Iout = ½*(id1-id2) = ½*(gm1*(Vin/2)-gm2*(-Vin/2)) = ½*gm1*Vin이고, Gm=1/2*gm1이 됩니다.
ii) Rout 구하기
Fig. 5.23(c)처럼, M2가 M1의 source output impedance인 Rdeg = 1/gm1||ro1에 의해 degeneration되었다고 볼 수 있습니다.

그러면 Rout = {(1+gm2ro2)(1/gm1||ro1)+ro2} || ro4인데, 대칭성과 근사에 의해 1+gm2ro2 ≈ gm1ro2, 1/gm1||ro1 ≈ 1/gm1이므로 Rout = (2ro2)||ro4가 됩니다.
따라서 Av 식은 (5.20)과 같게 됩니다.
만약 ro4가 ∞로 근사되면, Av는 –gm1ro2가 됩니다.

OTA의 Small-Signal Gain 구하기 - 방법 (2)
Small-signal gain을 구하는 두 번째 방법입니다.
Vout/Vin을 구하기 위해 Vp/Vin과 Vout/Vp를 구해서 곱하는 방법인데요.
i) Vp/Vin

Fig. 5.24처럼 M1을 source follower로 생각하면, Vp/Vin을 (5.21)과 같이 적을 수 있습니다.
여기서 Req는 M2의 source에서 본 저항으로, (5.22)와 같습니다.
(5.22)를 (5.21)에 대입하면 (5.23)과 같습니다.
ii) Vout/Vp
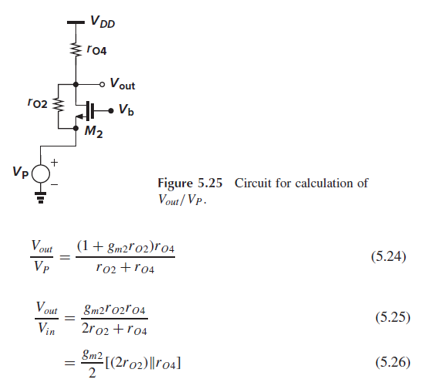
Fig. 5.25는 Vout/Vp를 구하기 위해 왼쪽 branch를 따로 그린 것입니다.
M2를 common-gate stage로 보면, Vout/Vp는 CG stage의 gain으로 (5.24)와 같습니다.
(5.23)과 (5.24)로부터 구한 Vout/Vin은 (5.26)이 됩니다.
Differential Pair with Active Load (5T OTA)
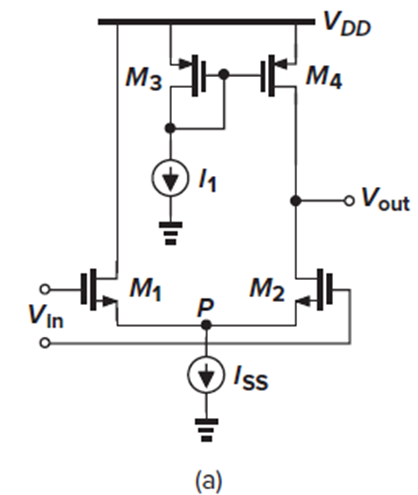
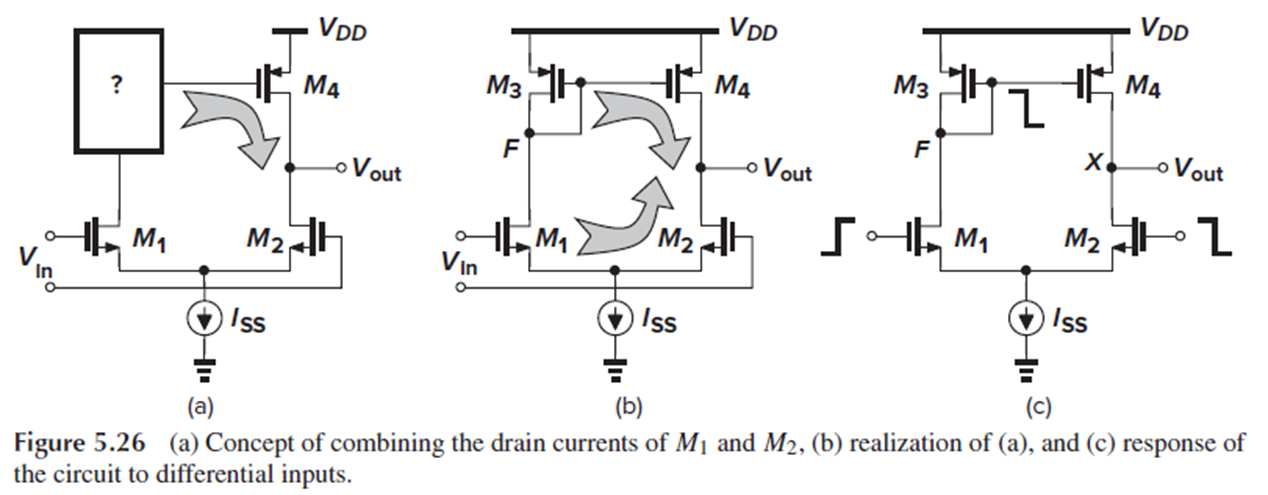
Fig. 5.23(a)의 differential pair with passive load에서는 M1의 small-signal drain current가 load에 흐르지 않고, output에도 영향을 미치지 않습니다.
우리는 Vin이 load와 Vout에 더 큰 영향을 미치도록, load의 gate voltage가 Vin에 따라 변하는 active load를 쓰고 싶습니다.
Fig. 5.26(b)에 나온 five-transistor OTA로 이를 구현할 수 있습니다.
여기서 M3와 M4는 동일한 transistor이고, active current mirror로 동작합니다.
즉, M1, M3, M4에 흐르는 Id가 동일합니다.
M3가 어떻게 gain을 높이는지 보기 위해, Fig. 5.26(c)처럼 M1과 M2의 Vg가 반대 polarity로 동일한 값만큼 변한다고 가정해 봅시다.
Id1이 증가하고, Id3도 따라 증가해야 하므로 M3의 Vgs가 증가하기 위해 Vf가 감소하고, Id2가 감소하겠죠. (왜 왼쪽 회로를 기준으로 설명? 오른쪽 회로에서는 Iout으로 전류가 빠져나갈 수 있어서 그럼?)
M3와 M4가 Vg를 공유하므로 Id4 역시 증가할 텐데, Id4는 증가하고 Id2가 감소하면 출력으로 흐르는 전류 Id4-Id2 = Id1-Id2가 증가하게 됩니다.
따라서, M1과 M2에 differential input을 가하면 Vout이 증가합니다.
여기서 M4의 Vg가 일정하기 때문에, M4는 Vout을 바꾸는 데에 active한 역할을 하지 않습니다.
Five-transistor OTA를 ‘differential pair with active load’라 부르기도 합니다.
5T OTA - Large-Signal Analysis
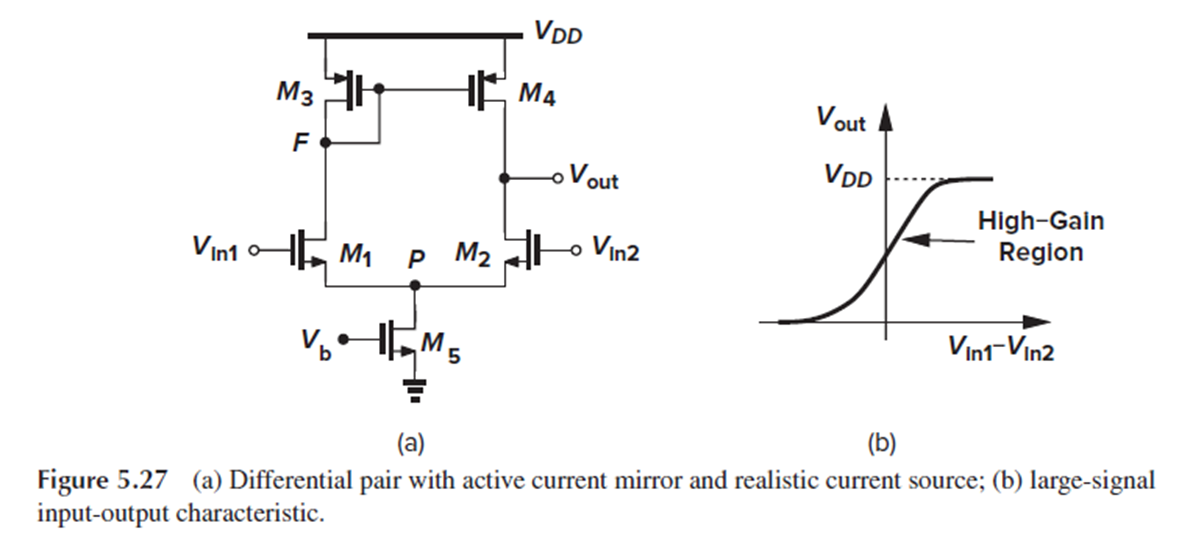
Five-transistor OTA의 large-signal behavior를 보겠습니다.
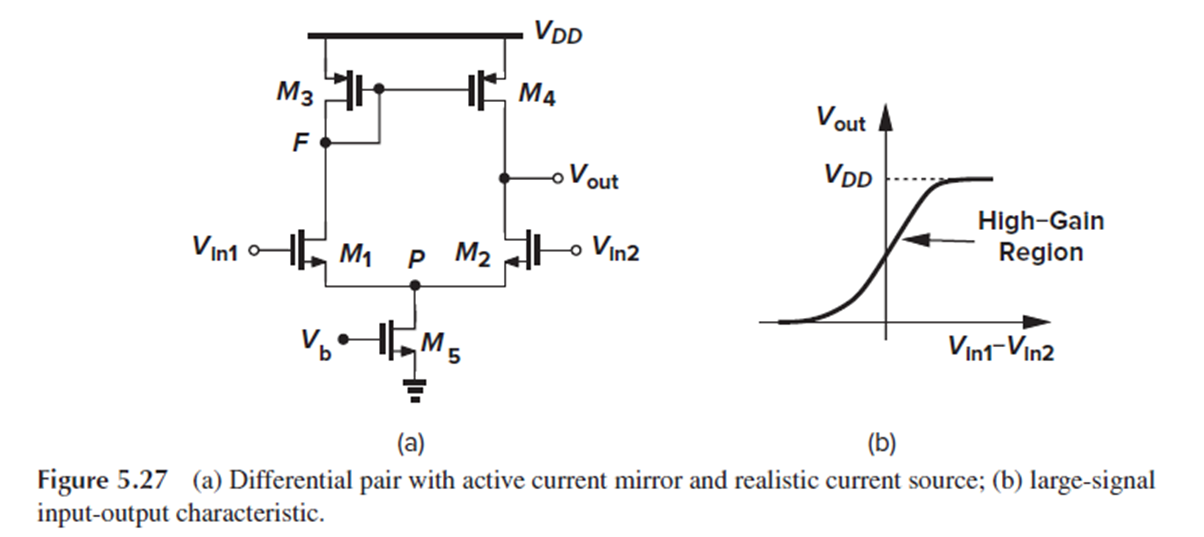
먼저 Fig. 5.27(a)처럼 ideal tail current source를 MOSFET으로 대체합니다.
- Vin1이 Vin2보다 훨씬 negative하다면 M1이 꺼지고, 따라서 M3와 M4도 꺼지게 됩니다.
- 그러면 Vdd로부터 전류가 흐르지 않으므로, M2와 M5는 deep triode region에서 동작합니다.
- 따라서 Vout=0입니다.
- Vin1이 Vin2에 가까워지면 M1이 켜져서 M3와 M4도 켜지고, 전류가 흐릅니다.
- 그러면 이제 Vout은 Id4-Id2에 비례하게 됩니다.
<Fig. 5.27(b) 설명>
- Vin1과 Vin2의 차이가 매우 작을 때는, M2와 M4가 둘다 saturation이며 gain이 큽니다.
- Vin1이 Vin2보다 커지면, Id1, |Id3|, |Id4|가 증가하고 Id2가 감소합니다.
- 그러면 Vout이 증가하고 M4를 triode region으로 drive합니다.
- Vin1-Vin2이 충분히 크다면, M2가 꺼지고, M4가 deep triode region에서 동작하여 전류가 흐르지 않고, Vout=Vdd가 됩니다.
- 만약 Vin1 > Vf+Vth라면(M1의 triode 조건), M1이 triode region에 진입합니다.
- 또한, Vout은 Vin1과 phase가 같으며(in-phase respect to Vin1) Vin2와 180° 차이가 납니다(180° out of phase with respect to Vin2).
5T OTA - Choice of Input Comon-Mode
Input common-mode voltage를 잘 고르는 것도 중요합니다.
M2가 saturation이려면, Vout > Vin,cm-Vth여야 합니다.
따라서, output swing이 최대이려면 Vin,cm이 최소여야 하며, Vin,cm의 최소값은 Vgs1,2+Vds5,min입니다.
이렇게 Vin,cm의 값에 제약이 걸렸다는 점이 5-transistor OTA의 단점입니다.
5T OTA - Symmetry
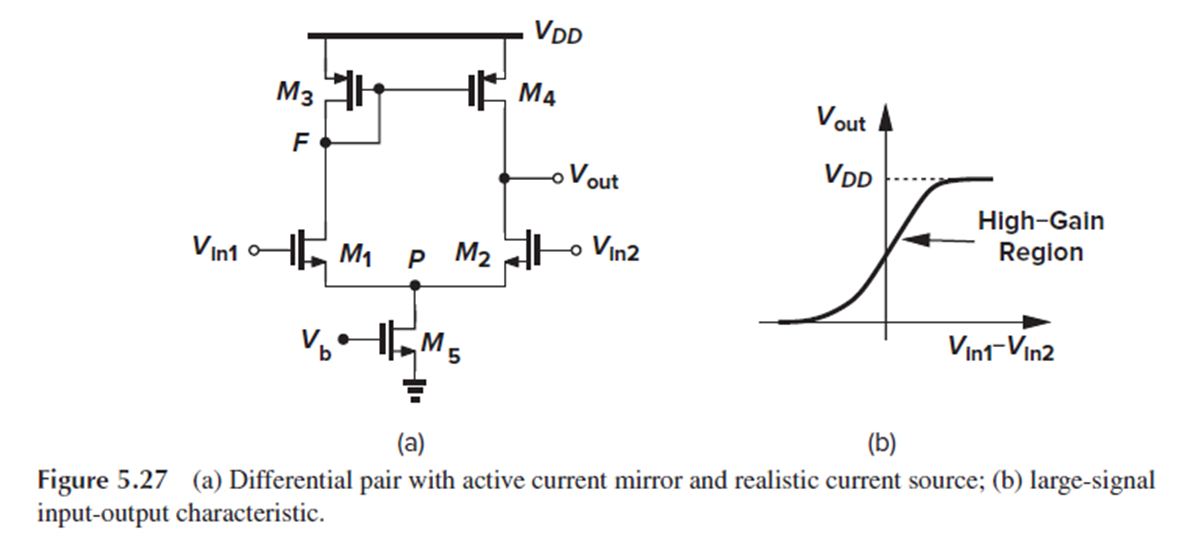
이 회로에서 Vin1=Vin2일 때 양쪽 회로가 symmetric하고, Vout=Vf=Vdd-|Vgs3|이 됩니다.
M3과 M4의 |Vgs|가 같으므로 Id3=Id4이고, M4의 |Vgs|와 Id가 정해졌으니 M4의 Vds가 자동으로 결정되기 때문입니다.
M4의 Vs는 Vdd로 고정이니 Vd인 Vout이 Vf과 같게 정해지겠죠.
그런데 실제로는 회로에 asymmetry가 생겨, Vout과 Vf 간 오차가 발생합니다.
그러면 M4 또는 M2가 triode region에 빠질 수 있습니다.
예를 들면, Vth2가 Vth1보다 약간 작은 asymmetry가 있을 때, Vin1=Vin2더라도 Id2가 Id1보다 약간 커지게 됩니다.
그러면 Vout이 확 작아집니다.
5T OTA는 asymmetry의 영향을 크게 받으므로, open-loop configuration에서 small signal을 증폭하는 데에는 잘 쓰이지 않습니다.
대신, large swing에 대해 differential input을 받아서 single-ended output을 내놓는 ‘differential to single-ended converter’로 쓰입니다.
다음 example에서 이에 대해 알아보겠습니다.
5T OTA - Differential to Single-Ended Converter

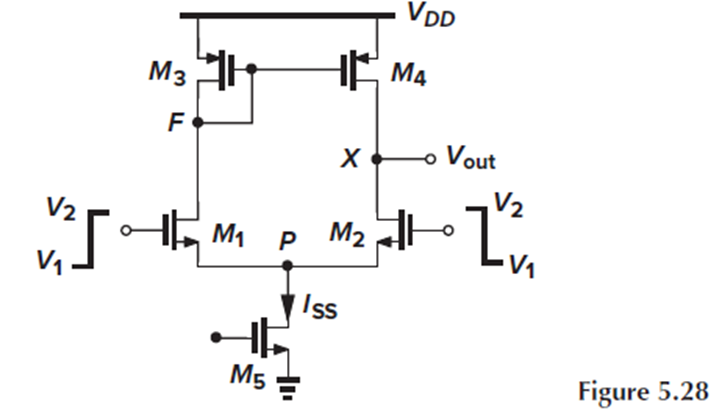
5T OTA는 differential signal을 single-ended rail-to-rail signal로 변환할 수 있습니다.
*Rail-to-rail: 신호가 전원 전압의 최저 rail(Vss)부터 최고 rail(Vdd)까지 완전한 전압 범위를 차지하는 신호
여기서 single-ended swing이 300mVpp, 즉 V2-V1=300mV입니다.
그리고 이 swing이 M1과 M2 중 하나를 끌 수 있도록 M1과 M2의 (W/L)과 Iss를 조절합니다.
M1에 Iss가 모두 흐르면, M2가 꺼져서 오른쪽 회로에는 전류가 흐르지 않습니다.
따라서 Vout=Vdd가 됩니다.
반대로 M1, M3, M4가 꺼지면, M2와 M5는 켜져있더라도 전류가 흐르지 않고 Vout=0이 됩니다.
이처럼 5T OTA는 output에서 rail-to-rail signal swing을 만들어낼 수 있습니다.
5T OTA - Op Amp

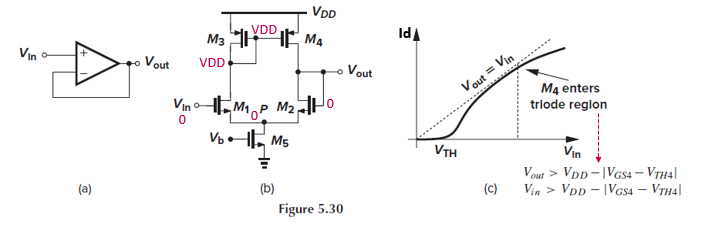
5T OTA로 op amp를 만들 수 있습니다.
Fig. 5.30(a)는 unity-gain buffer라고 하는, gain이 1인 op amp입니다.
Vin-에 Vout을 연결하는 구조로, 이를 5T OTA로 구현한 schematic은 Fig. 5.30(b)입니다.
이 회로의 large-signal input-output 특성은 Fig. 5.30(c)와 같습니다.
Vin=0일 때 M1, M3, M4는 꺼져 있습니다. M4가 꺼져있으니 M2에 전류가 흐르지 않고, M5에도 전류가 흐르지 않겠죠.
따라서 Vout=Vp=0입니다.
Vin이 증가하다가 Vth를 넘으면, M1에 Id가 흐르기 시작하고, M3, M4, M2에도 전류가 흐릅니다.
M3과 M4는 current mirror를 구성하므로 Id3≈Id4이기 때문에, Id1≈Id2이고 Vgs1≈Vgs2입니다.
즉, Vout≈Vin이 되어 unity gain을 얻을 수 있습니다.
Vin이 높아지다가 Vdd-|Vgs4-Vth4|보다 높아지는 시점에서 M4가 triode region에 진입하게 됩니다.
5T OTA - Small-Signal Analysis
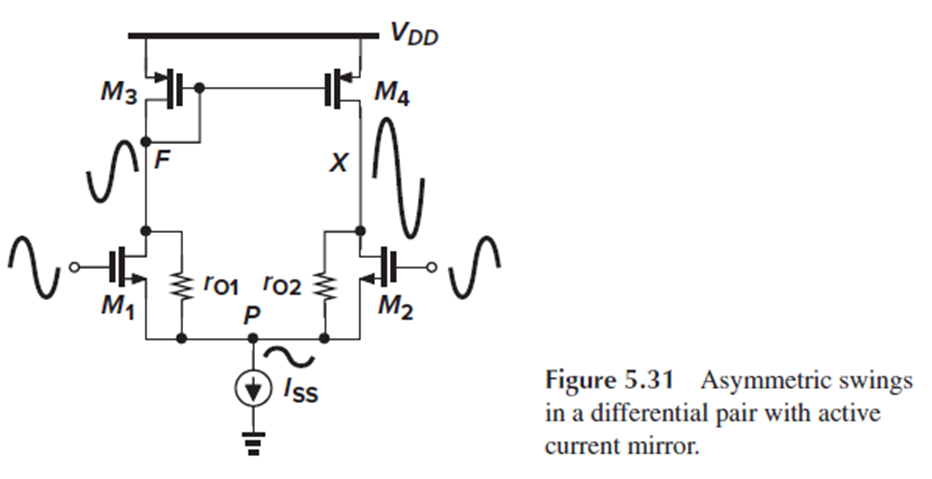
이번에는 5T OTA의 small-signal 특성을 알아보겠습니다.
Fig. 5.31의 5T OTA 회로에 바로 half-circuit concept를 적용하기에는 무리가 있습니다.
Node F와 X에서의 voltage swing이 달라서 node F와 X가 node P에 미치는 영향이 서로 상쇄되지 않아, node P가 virtual gnd가 아닐 수 있기 때문입니다.
따라서 Av = Gm*Rout 식으로 gain을 구해야 합니다.
Approximate analysis와 exact analysis로 Av=Gm*Rout을 구해볼 것입니다.
Approximate analysis에서는 node P를 virtual gnd로 근사해서 half-circuit concept를 적용하고, exact analysis에서는 정석대로 풀이합니다.
Approximate Analysis
i) Gm 구하기
Gm을 구하기 위해 Fig. 5.32(a)처럼 output을 접지시킵니다.
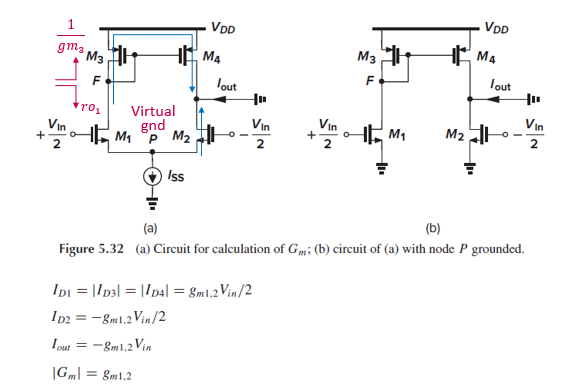
Node F에서 본 impedance는 M3 쪽으로 1/gm3, M1 쪽으로 ro1입니다.
M3 쪽으로 전류가 훨씬 쉽게 흐를 수 있는 것이죠.
반면, X에서 ro1을 거쳐 P로 흐르는 전류는 무시할 수 있을 정도로 작으므로, node P가 virtual ground로 근사될 수 있습니다.
(이후 exact analysis에서는 node P를 virtual ground로 근사하지 않습니다.)
그러면 회로가 Fig. 5.32(b)처럼 그려집니다.
따라서 M1, M3, M4의 small-signal 전류가 gm1,2*Vin/2로 같고, M2의 small-signal 전류는 –gm1,2*Vin/2입니다.
그러면 Iout = Id2-Id4 = -gm1,2*Vin이고, Gm = Iout/Vin = gm1,2가 됩니다.
ii) Rout 구하기
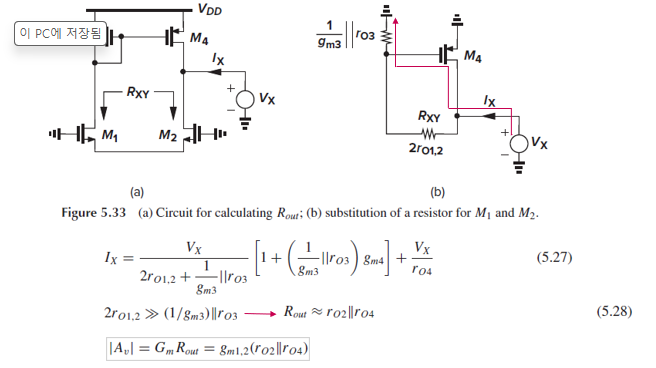
이번에는 Rout을 구해보겠습니다.
Rout을 구하기 위해 test voltage Vx를 연결하고, test current Ix를 흘립니다.
아까 small-signal 전류가 node P 쪽으로 흐르지 않는다고 했으니, small-signal 관점에서는 Iss가 open입니다.
그래서 회로를 Fig. 5.33(a)처럼 그릴 수 있습니다.
M1에 흐르는 전류가 모두 M2에 흐르게 됩니다.
M1과 M2의 gate voltage가 gnd이므로 이 두 트랜지스터를 저항 Rxy = 2ro1,2로 보겠습니다. (Fig. 5.33(b))
그러면 test current Ix가 Rxy를 통해 M3에 흐르고, current mirror에 의해 M4에도 Ix가 흐르게 됩니다.
Ix의 식은 (5.27)과 같습니다.
Rxy와 M3를 통해 흐르는 small-signal current는 Vx/[2ro1,2+(1/gm3)||ro3]입니다.
M4에 흐르는 small-signal current는 gm4*Vgs4+Vx/ro4인데, Vgs4가 Vx/[2ro1,2+(1/gm3)||ro3]*[((1/gm3)||ro3)gm4]입니다.
따라서 붉은 화살표를 따라 KVL을 적용하면 Ix를 (5.27)로 구할 수 있습니다.
여기서 2ro1,2 >> (1/gm3) || ro3이면 Rout이 ro2||ro4로 근사됩니다.
Exact Analysis
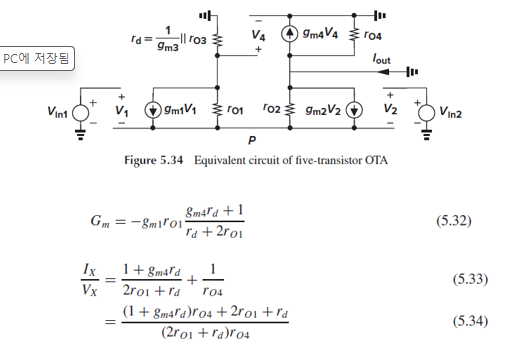

이번에는 node P가 virtual gnd라고 가정하지 않고, 5T OTA의 small-signal equivalent circuit을 그려 정석대로 gain을 구하는 방법입니다.
Gain이 (5.38)로 구해지는데, 이전에 approximation analysis로 구했던 gain인 gm1,2(gm2||ro4)와 비교했을 때 correction factor가 추가되었습니다.
이 correction factor는 1보다 작습니다.
5T OTA를 사용하는 이유

Fig. 5.35의 회로는 5T OTA와 gain이 비슷합니다.
심지어 Fig. 5.35의 회로가 gain이 더 큽니다.
그럼에도 불구하고 5T OTA를 사용하는 이유는 differential operation이 CM noise에 덜 민감하고, 신호 왜곡이 덜하기 때문입니다.
Headroom Issues
5T OTA는 저전력으로는 잘 사용되지 않습니다.
5T OTA에 쓰이는 diode-connected PMOS가 voltage headroom을 잡아먹기 때문입니다.
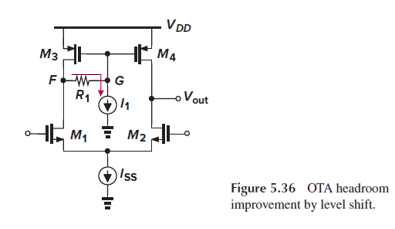
Headroom을 늘리기 위해, Fig. 5.36처럼 F와 M3의 gate 사이에 저항 R1을 추가하고, M3의 gate에 current source I1을 연결합니다.
그러면 Vg가 Vf-R1*I1만큼 작아집니다. (이때 R1*I1 ≤ Vth3)
Vg가 작아지면 input CM level이 높아져서, 이전 stage 회로의 설계가 쉬워집니다.
이때, I1으로 인한 asymmetry가 너무 크지 않도록, I1은 Iss/2보다 훨씬 작아야 합니다.
Common-Mode Properties
Input CM level에 변화가 생기면 모든 transistor의 bias current가 변합니다.
만약 CM gain이 생기면 input CM level이 변해서 output signal이 clipping된다거나 하는 문제가 발생할 수 있습니다.
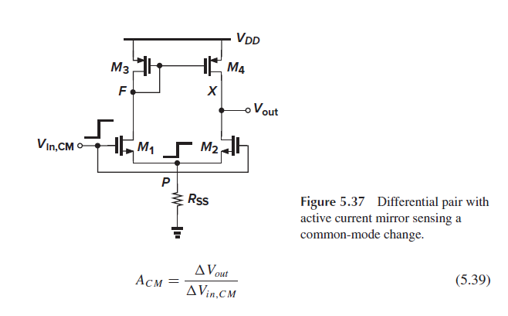
Fig. 5.37의 CM gain은 input CM 변화에 의해 생긴 single-ended output component로, (5.39)로 나타납니다.
만약 transistor들이 symmetric하다면, 모든 input CM level에 대해 Vout=Vf입니다.
예를 들어, Vin,cm이 증가하면 Vf가 감소하고, Vout도 감소합니다.
Vout=Vf이면 두 node를 short시킬 수 있겠죠.
Common-Mode Properties
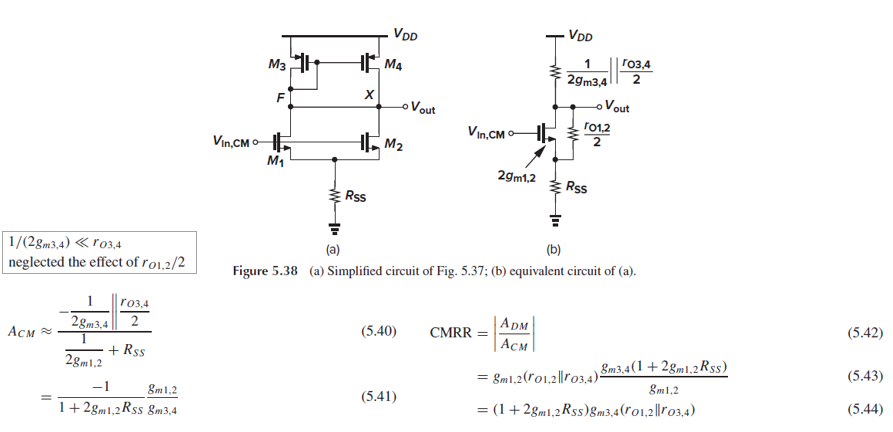
두 node를 short시키면 Fig. 5.38(a)가 되고, equivalent circuit은 Fig. 5.38(b)와 같습니다.
M1과 M2, M3와 M4는 병렬인 점을 반영했습니다.
여기서 common-mode gain은 (5.41)이 됩니다.
Rss=ro이고 2gm1,2ro>>1이라면, CMRR은 (gmro)^2꼴이 됩니다.
Mismatch의 효과
다음으로, mismatch가 있을 때의 common-mode gain을 보겠습니다.
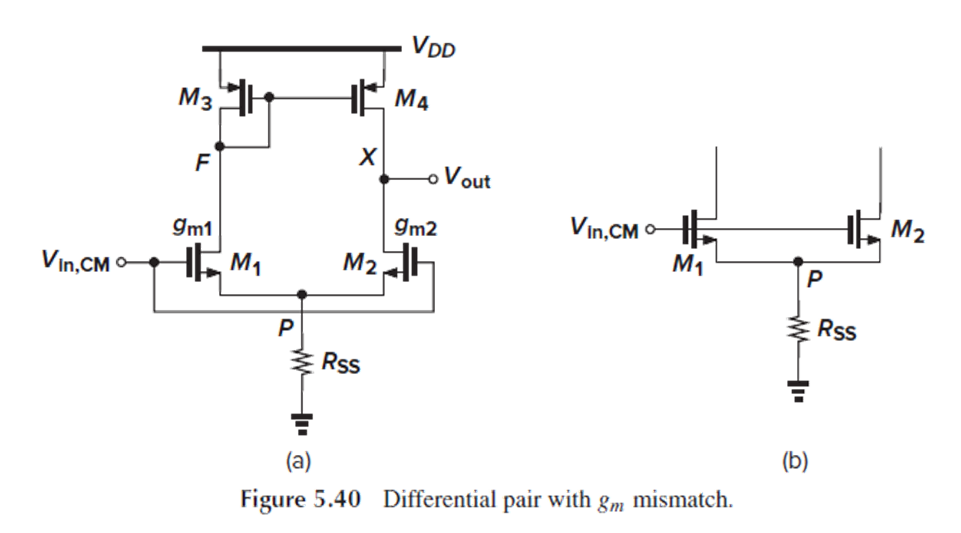
Fig. 5.40에는 M1과 M2의 gm mismatch가 있습니다.
gm1≠gm2라는 것입니다.
Node F와 node X의 전압 변화가 비교적 작기 때문에(?), ro1과 ro2의 효과를 무시한 채(왜 무시할 수 있는 것?) Id1과 Id2의 변화를 계산할 수 있습니다.
(Fig. 5.40) M1과 M2를 transconductance가 gm1+gm2인 하나의 transistor로 간주하고, 이를 source follower로 생각하여 node P에서의 전압 변화를 (5.50)으로 구할 수 있습니다.
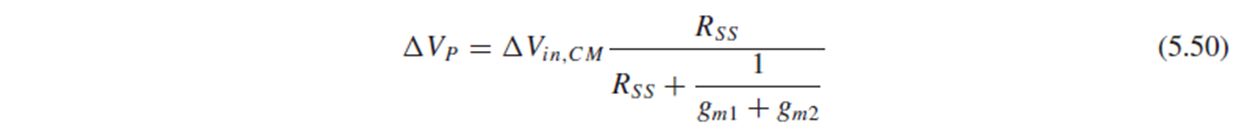
M1과 M2에서의 전압 변화는 (5.51)~(5.54)로 구해집니다.
ΔId1에 (1/gm3)||ro3를 곱하면 M4의 Vgs가 되고, 여기에 gm4를 곱한 gm4*[(1/gm3)||ro3]*ΔId1이 M4의 small-signal current가 됩니다.
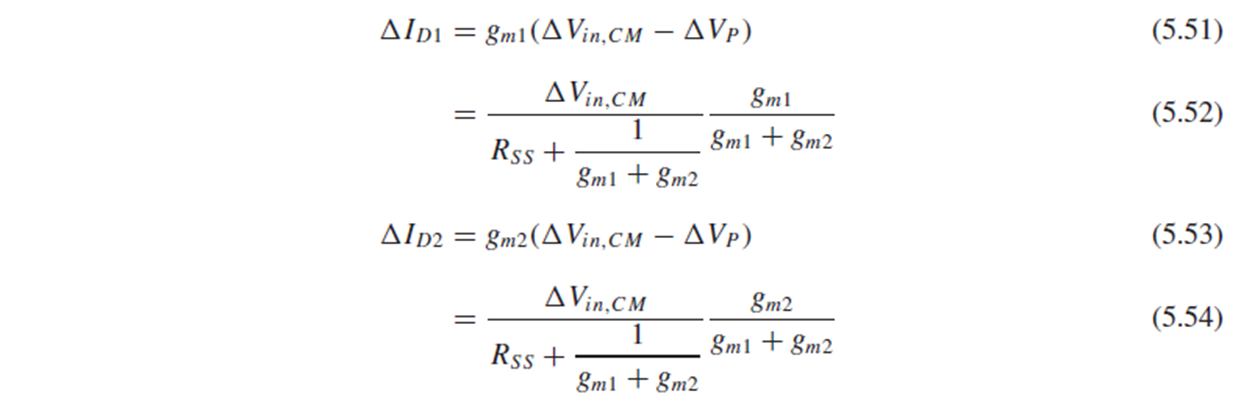
ΔId4와 ΔId2의 차가 output impedance인 ro4로 흐릅니다. (ro1과 ro2의 영향을 무시했기 때문)
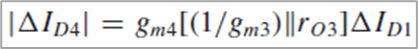
따라서 ΔVout은 (5.55), (5.56)이 되고, ro3>>1/gm3을 가정하면 common-mode gain은 (5.57)이 됩니다.

Mismatch가 없을 때의 common-mode gain인 (5.41)과 비교했을 때, mismatch가 생김으로써 (gm1-gm2)ro3 항이 추가되었습니다.
5T OTA의 기타 특성
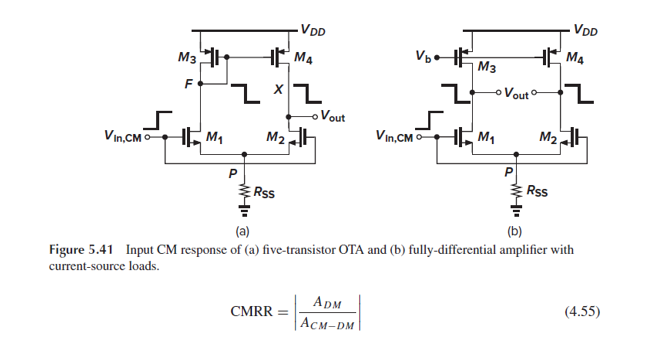
Fig. 5.41(a)
- Five-Transistor OTA에서 input common-mode 변화가 Vout에 영향을 미쳐서, 회로의 CMRR이 유한한 문제가 발생합니다.
- CMRR은 differential circuit에서 의도한 gain Adm을 원치 않는 gain Acm-dm으로 나눈 값으로, Acm-dm이 0이고 CMRR이 ∞여야 좋은 거죠.
Fig. 5.41(b)
- Fully-diferential한 회로는 input common-mode 변화를 무시하고, differential-mode만을 증폭합니다.
- 따라서 Vout이 common-mode input에 영향을 받지 않고, CMRR이 높아서 5T OTA보다 성능이 좋습니다.
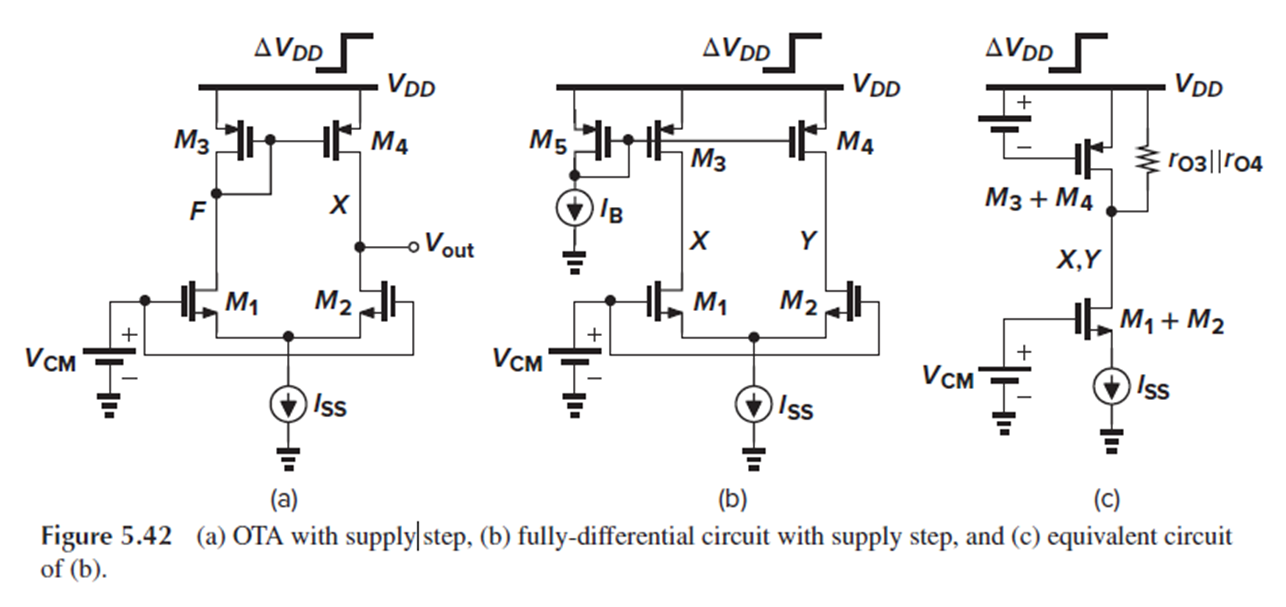
Fig. 5.42(a)
- Five-Transistor OTA에서 VDD 변화에 따라 Vout도 동일하게 변화하여 supply rejection 성능이 낮습니다.
- Vdd를 ΔVdd만큼 조금 변화시켰을 때, ΔVf가 ΔVdd만큼 변화합니다.
- M1의 input이 Vcm으로 일정해서 M1이 current source와 같기 때문에, Vgs3=Vf-Vdd도 일정해야 하기 때문입니다.
- 회로가 symmetric하므로 Vout도 ΔVdd만큼 변하게 되며, 이는 supply rejection이 잘 되지 않음을 나타냅니다.
Fig. 5.42(b)
- 반면, fully-differential한 회로는 supply rejection 성능이 좋습니다.
- Vgs5, Vgs3, Vgs4가 일정하므로 Vx와 Vy가 같은 양만큼 변화하여, differential output은 변하지 않습니다.
Fig. 5.42(c)
- 따라서 X와 Y를 short하고, M3와 M4를 합치고, M1과 M2도 합칠 수 있습니다.
- 그러면 cascode 구조가 된다는데, 어디가 cascode 구조이고 어느 부분의 output impedance가 높다는 건지는 잘 모르겠습니다. (???)



