출처: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 6 - Frequency Response of Amplifiers (pg. 173~180, 203~206)
6. Frequency Response of Amplifiers
6.1. General Considerations

- MOSFET에는 Cgs, Cgd, Cdb, Csb 의 parasitic capacitance가 존재하며, 회로의 주파수 응답 분석을 복잡하게 만듭니다.
- 이를 단순화하기 위해 Miller 정리와 극점(pole)을 노드에 연관시키는 방법 같은 근사 기법이 사용됩니다.
- 주파수 응답은 H(jω)로 표현되며, 크기(magnitude)와 위상(phase) 정보를 담고 있습니다.
- Bode의 법칙에 따르면 주파수 응답은 극점을 지나면 −20dB/decade로 감소하고, 영점을 지나면 +20dB/decade로 증가합니다.
- 이 장에서는 근사 기법과 특정 조건(예: 부하 커패시턴스가 매우 작거나 클 때)을 사용하여 복잡한 전송 함수의 분석을 단순화합니다.
6.1.1. Miller Effect
Miller's Theorem

Fig. 6.2(a)와 (b)가 서로 같은 회로라고 해 봅시다.
Z1은 X 쪽에서 본 Z, Z2는 Y 쪽에서 본 Z입니다.
Z에 흐르는 전류는 (Vx-Vy)/Z인데, Fig. 6.2(a)와 (b)가 서로 같은 회로이려면 Z1과 Z2에도 같은 전류가 흘러야 합니다.
따라서 Z1, Z2는 (6.2), (6.3)이 됩니다.
여기서 Vy/Vx를 Av로 두었습니다.

Cf의 Z는 1/sCf입니다.
Miller effect에 의해 Z1는 1/sCf를 (1+A)로 나눈 값, 즉 Z1=1/[sCf(1+A)]가 됩니다.
이는 Cf가 Cf(1+A)로 된 효과와 같으며, 이를 capacitor의 Miller multiplication이라고 합니다.
실은, input(X)에서 전압이 ΔV만큼 변했다면, ouptut(Y)에서는 전압이 -AΔV만큼 변할 테고,
따라서 Cf 양단의 전압차가 (1+A)ΔV이므로 Cf에 저장되는 전하가 Cf(1+A)ΔV인 것입니다.
그런데 input(X) 쪽에서 볼 때는 ΔV만큼의 전압 변화에 Cf에 저장되는 전하가 Cf(1+A)ΔV이므로, Cf가 Cf(1+A)로 보이는 것이죠.
Miller Effect가 성립하지 않는 조건

만약 node X에서의 capacitance를 (A+1)Cf로 만들고 싶다면, gain이 –A인 amplifier를 사용하면 됩니다.
그러려면 node Y에서의 swing이 AV0이어야 하는데, AV0가 amplifier의 동작 범위 내에 있어야 하겠죠.
따라서 이것이 가능할 때만 Miller 정리가 가능합니다.
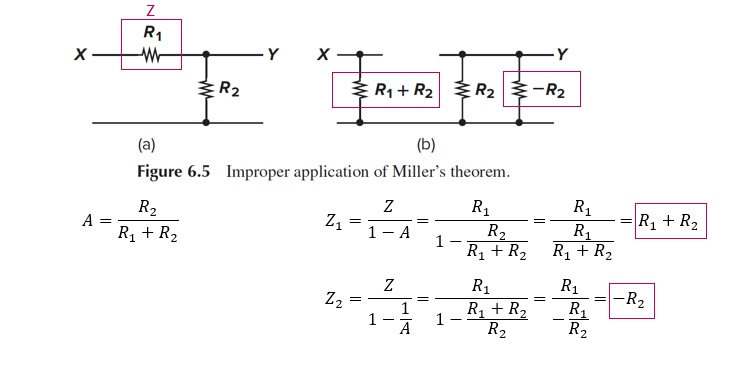
Figure 6.5는 Miller 정리가 타당하지 않은 경우입니다.
아까와 달리 Z가 input과 output 사이의 유일한 신호 경로에 있습니다.
이때 Miller 정리에 따라 X에서 본 impedance는 R1+R2, Y에서 본 impedance는 –R2가 됩니다,
Y에서는 물리적인 impedance R2와 Miller 법칙에 의한 –R2가 병렬로 존재합니다.
이렇게 Z가 input과 output 사이의 유일한 신호 경로에 있을 때, input impedance는 의도한 대로 얻었지만 gain이 정확하지 않게 됩니다.
Miller Effect가 성립하는 조건

Miller 정리를 적용할 수 있는 조건은, Figure 6.6과 같이 Z가 main signal path와 병렬로 연결되었을 때입니다.
Miller's Approximation

지금까지 A=Vy/Vx를 Miller 정리 식에 대입했는데, 고주파로 가면 이게 성립하지 않습니다.
고주파에서는 output단의 parasitic cap에 의해 Rout 값이 감소하고, 신호가 Cf와 Rout에 분배되기 때문입니다.
즉, A(s)=Vy/Vx를 사용해야 합니다.
고주파에서 Vy≠-AVx가 되므로, Miller 정리를 단순히 적용할 수는 없지만, 저주파에서의 gain인 A를 이용해서 회로의 동작을 근사적으로 분석할 수 있습니다.
이를 Miller 근사라고 합니다.

DC에서 Rs에 흐르는 전류가 (Vin-Vx)/Rs, Rout의 voltage drop이 (Vin-Vx)Rout/Rs입니다.
따라서 KVL에 의해 (6.7) 식이 나옵니다.
AC에서 Cf에 흐르는 전류도 (Vin-Vx)/Rs이고, 이는 (Vx-Vout)sCf과 같습니다. (6.8)
(6.7)을 Vx에 대해 정리하여 (6.8)에 대입하면 (6.9)의 transfer function을 얻습니다.
Transfer function을 통해 회로의 zero 𝜔z와 pole 𝜔p를 알 수 있습니다.
Fig. 6.9(b)는 |𝜔p| < |𝜔z|의 경우를 plot한 것입니다.

Miller 근사에 의하면, Cf는 input에서 (1+A)Cf가 되고, output에서 (1+1/A)Cf가 됩니다.
이를 바탕으로 transfer function을 구해보면, direct analysis의 결과와 달리 pole만 2개인 것으로 예측되었습니다.
이렇게 Miller 근사로 완벽하게 예측하지 못하는 경우도 있지만, 대체로 회로의 동작에 대한 직관을 얻을 때 유용합니다.
또한, Miller approximation은 output impedance를 정확하게 계산하지 못합니다.

Rin=∞, Rout=ro라고 알고 있는 위 회로에서, Miller approximation을 사용하여 Rin, Rout을 구해 보았습니다.
Rin은 ∞로 계산되었지만, Rout은 원래 값과 다르게 계산된 것을 볼 수 있습니다.
따라서 Miller approximation의 한계를 아래와 같이 정리할 수 있겠습니다.
- Zero를 예측하지 못할 수 있다.
- Pole을 실제보다 더 많이 예측할 수 있다.
- Output impedance를 정확하게 계산하지 못할 수 있다.
Pole과 Node의 상관관계

이 예시를 보면 각 node가 하나의 pole을 만든다고 생각할 수도 있지만, 꼭 그렇지는 않습니다.

이런 회로 같은 경우에는 R3와 C3이 한 node에만 연결된 게 아니라 두 node X, Y와 상호작용합니다.
따라서 한 node당 pole이 존재한다고 할 수는 없습니다.
그럼에도, 한 node당 1개의 pole이 존재한다는 가정은 transfer function을 예측하는 데에 직관을 줍니다.
관심있는 node로부터 ground까지의 equivalent capacitance와 equivalent resistance를 곱하면, time constant와 pole frequency를 얻을 수 있습니다.

Common-gate stage의 transfer function을 구하는 과정입니다.
Node X와 Y에 각각 pole이 있다고 가정하고 ωin, ωout을 구하고, magnitude를 구해 transfer function을 완성합니다.
6.7 Gain-Bandwidth Trade-Offs
Amplifier 설계에서 gain과 bandwidth를 동시에 극대화하는 것이 중요하며, 특히 optical communication에서는 높은 gain과 넓은 bandwidth가 필요합니다. High-speed 설계에서는 gain과 bandwidth 간의 tradeoff를 고려해야 합니다.
-3dB bandwidth(ω_−3dB)과 "unity-gain" bandwidth(ω_u)가 중요합니다.

Gain-Bandwidth Product(GBW)

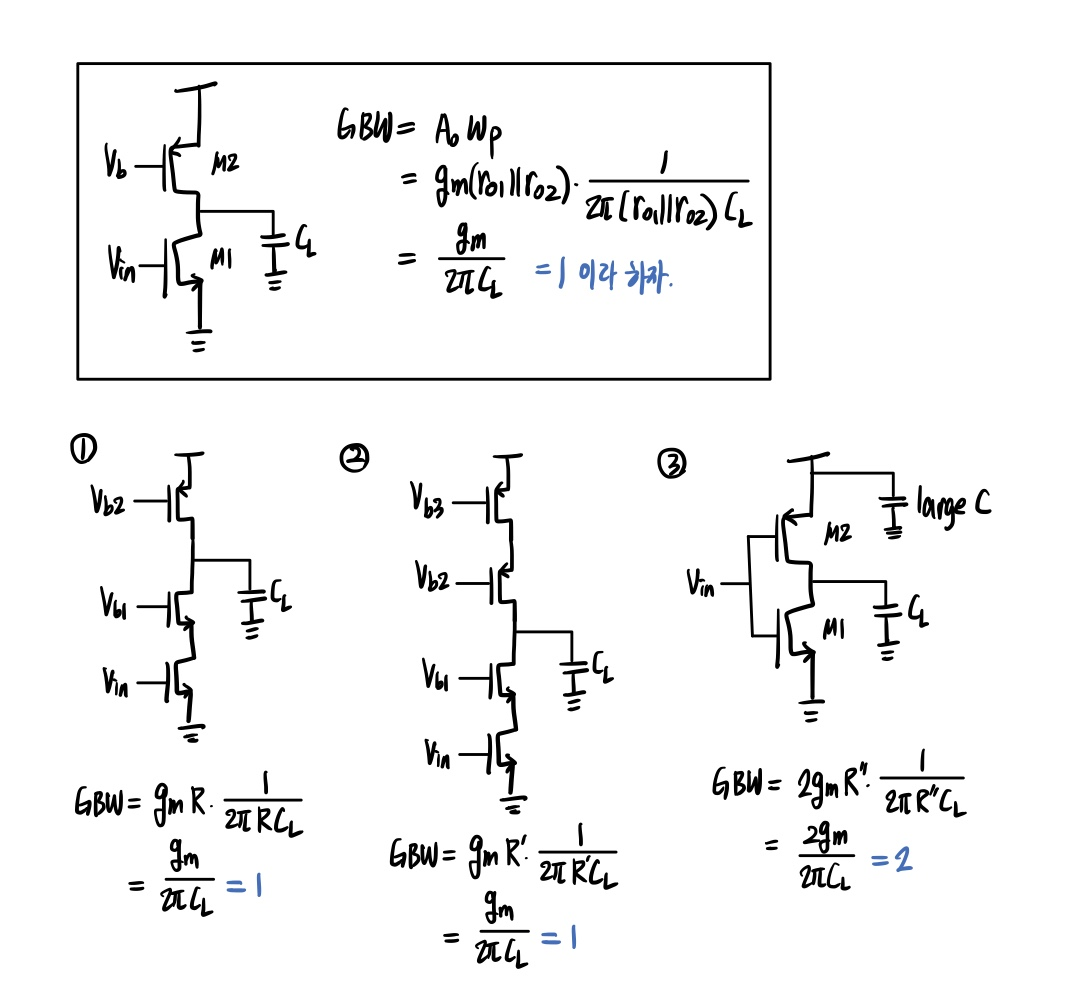
Gain-bandwidth product는 이름처럼 gain과 bandwidth를 곱한 것으로(6.98), Fig. 6.44와 같이 pole이 1개인 CS stage의 경우, (6.99)처럼 나타내지며 최종적으로 (6.100)의 꼴이 됩니다.
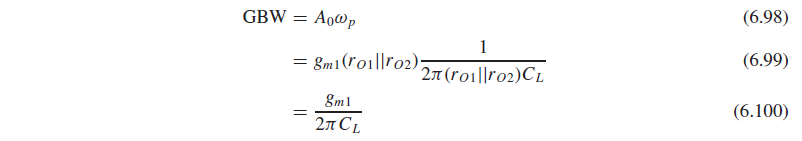
GBW가 gm/C의 꼴이 되는 것을 확인할 수 있으며, GBW는 클수록 좋습니다.
One-pole system에서는 GBW가 unity-gain bandwidth와 거의 같은 값입니다.
이를 증명해 봅시다.
One-pole system에서 전달함수 H(s)는 아래와 같습니다.

여기서 A0는 DC gain, 𝜔p는 dominant pole frequency, s=j𝜔로 복소 주파수입니다.
Frequency domain에서 s=j𝜔를 대입하면 아래와 같고,

분모의 크기를 계산하면

이고, 따라서 주파수 응답의 magnitude는 다음과 같이 표현됩니다.

Unity-gain bandwidth는 magnitude가 1일 때의 𝜔이며, 해당 𝜔를 𝜔u라고 하면 (6.101) 식을 얻습니다.
(6.101)을 정리하고(6.102), A0가 매우 크다고 가정하면 unity-gain bandwidth 𝜔u ≈ A0*𝜔p로 (6.98)의 GBW와 비슷한 값이 됩니다.


아래 그림은 (왼)다양한 회로에서의 GBW 값 계산 예제 3개와, (오)회로의 Gm을 구하는 방법 및 예제 5개입니다.