출처: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 2 - Basic MOS Device Physics (pg.20~22)
2.3. Second-Order Effects
이 단원 전까지는 MOS 구조를 쉽게 이해하기 위해, 실제 아날로그 회로와는 맞지 않는 여러 가지 가정을 붙였습니다.
이 단원에서는 실제 회로 동작에 가깝고, 이후의 회로 분석에 매우 중요한 4개의 second-order effect를 알아볼 것입니다.
바로 body effect, channel-length modulation, subthreshold conduction, punch-through입니다.
이 포스팅에서는 이 중 body effect에 대해 알아보겠습니다.
다른 second-order effect에 대한 내용은 아래 링크들에 정리되어 있습니다.
2024.10.06 - [반도체 소자] - [Razavi][Ch2] MOSFET Second-Order Effects(2) - Channel Length Modulation
[Razavi][Ch2] MOSFET Second-Order Effects(2) - Channel Length Modulation
출처: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second EditionChapter 2 - Basic MOS Device Physics (pg.23~24)2.3. Second-Order Effects이 단원 전까지는 MOS 구조를 쉽게 이해하기 위해, 실제 아날로그 회로와는 맞
soobdal.tistory.com
2024.10.06 - [반도체 소자] - [Razavi][Ch2] MOSFET Second-Order Effects(3) - Subthreshold Conduction
[Razavi][Ch2] MOSFET Second-Order Effects(3) - Subthreshold Conduction
출처: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second EditionChapter 2 - Basic MOS Device Physics (pg.24~26)2.3. Second-Order Effects이 단원 전까지는 MOS 구조를 쉽게 이해하기 위해, 실제 아날로그 회로와는 맞
soobdal.tistory.com
[Razavi][Ch2] MOSFET Second-Order Effects(4) - Voltage Limatations, Punch-Through
출처: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second EditionChapter 2 - Basic MOS Device Physics (pg.26)2.3. Second-Order Effects이 단원 전까지는 MOS 구조를 쉽게 이해하기 위해, 실제 아날로그 회로와는 맞지
soobdal.tistory.com
Body Effect
이전 논의에서는, Figure 2.10과 같이 MOSFET의 bulk(substrate)와 source가 ground에 연결된 경우를 살펴봤습니다.
Vg = Vth에서 inversion layer가 생성되었죠.
그런데 만약 Figure 2.22와 같이, NMOS의 bulk 전압이 source 전압보다 낮아지면 어떤 일이 발생할까요?
S와 D junction이 reverse-biased 되어있기에(S/D에 positive bias, p-substrate에 negative bias) MOSFET이 정상 작동 하기는 하겠지만, 동작 특성이 조금 바뀔 수 있습니다.
이 효과를 이해하기 위해, 몇 가지 가정을 하겠습니다.
Vs = Vd = 0이고, Vg < Vth라서 gate 아래에 depletion region이 생성되긴 하지만 inversion layer는 없는 상태라고 가정하겠습니다.
Vb가 더 negative해질수록, 더 많은 hole들이 인력에 의해 bulk에 붙을 것이고, 이에 따라 gate와 substrate의 계면에는 negative charge(편의상 '전자층')가 남게 됩니다.
즉, Figure 2.23에서 보듯이, Vb = 0 인 왼쪽 경우보다 Vb < 0 인 오른쪽 경우에서 전자층이 더 두꺼워지는 것입니다.
*여기서 gate 아래에 형성된 전자층은 channel이 아닙니다.
이 상황에서 양의 gate 전압을 걸어 channel을 만들려 할 때, source의 전자와 gate 아래의 전자층의 척력이 작용해서 channel이 형성되기 어려워집니다.
Channel이 형성되려면 더 큰 gate 전압을 걸어줘야 하겠죠. Vth가 증가한다는 말과 같습니다.
이처럼 Vb < 0일 때 Vth가 증가하는 현상을 "body effect" 또는 "back-gate effect"라고 합니다.
이전에 살펴본 수식 2.1에 의하면, threshold voltage Vth는 depletion region에 있는 total charge Qdep(Qd)에 대한 함수입니다.
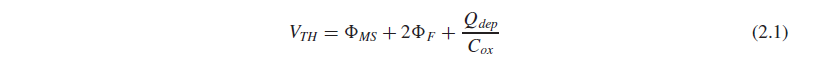
따라서, Figure 2.23의 오른쪽 그림처럼 Vb가 감소하여 Qd가 증가하면, Vth도 따라 증가하게 됩니다.
Body effect를 반영한 Vth 값은 아래와 같은데, 교재에도 이에 대한 증명은 없습니다.
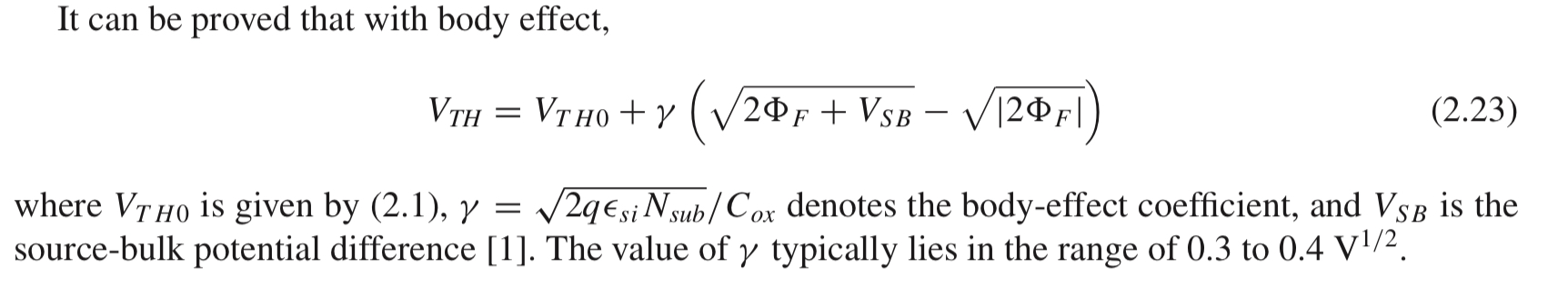
Body Effect가 회로에 미치는 영향
Body effect가 나타나려면, bulk potential Vsub이 바뀌면 안 됩니다. (Vsub이 Vb와 같은 의미로 쓰인 것 같습니다...)
만약 Vs가 Vsub에 따라 변화한다면, 같은 효과가 나타납니다.
예를 들어, Figure 2.25(a)의 회로에서 우선 body effect가 없다고 생각해 봅시다. Vth가 일정하다는 말입니다.
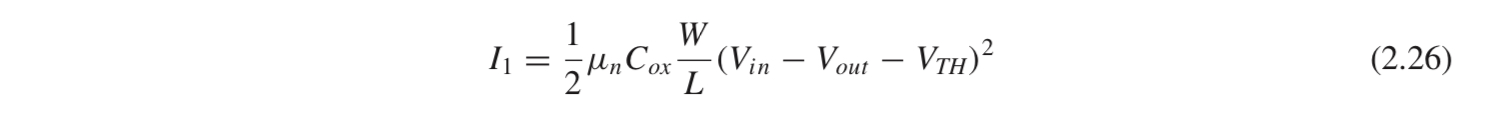
수식 2.26을 보면, I1, Vth가 일정하므로 Vin - Vout도 일정할 것입니다.
따라서 Vin이 변할 때, Vout은 Vin과 거의 일정한 차이를 두고 따라올 것입니다.
M1의 drain current가 current source의 전류 I1과 같아지도록 source 전압이 세팅되겠죠.
이를 그래프로 나타내면 Figure 2.25(b)처럼 됩니다.
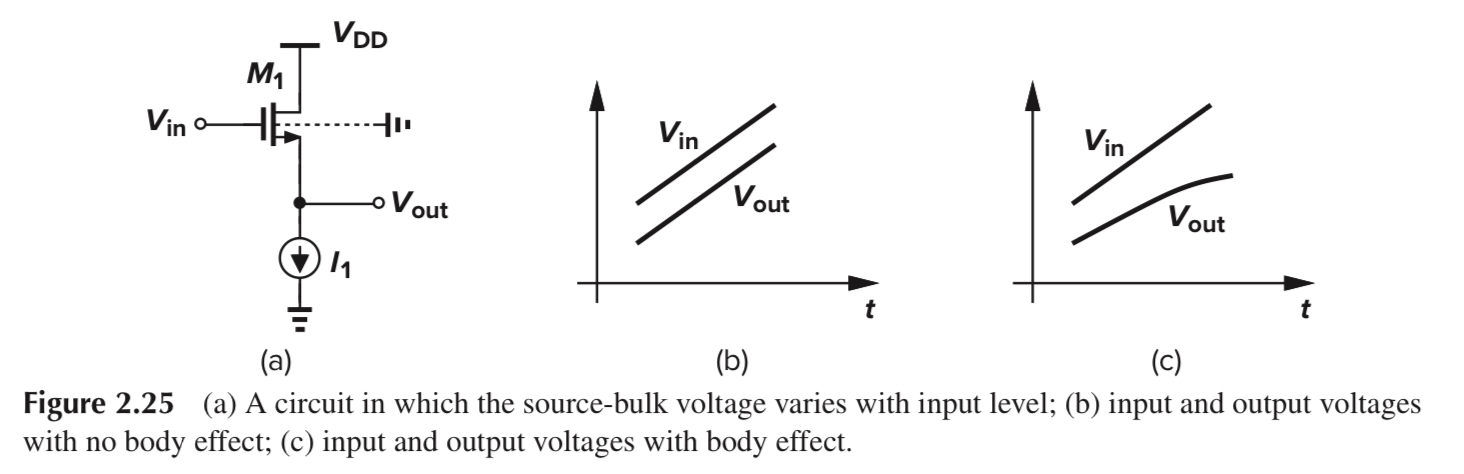
이제, substrate가 ground에 연결되어 있고, body effect를 무시할 수 없다고 가정합시다.
그러면, Vin과 Vout이 더 positive해질수록, source와 bulk의 전압차가 증가하여 Vth도 증가할 것입니다.
수식 2.26에 의해, M1의 Id가 current source의 전류 I1으로 일정하려면 Vin - Vout도 Vth만큼 증가해야 합니다.
Body effect가 존재할 때 Vin - Vout이 점점 커지는 효과는 Figure 2.25(c)의 그래프처럼 나타납니다.
Body effect는 최소화되는 것이 좋습니다.
Threshold voltage의 변화는 아날로그 회로 설계를(디지털 회로 설계마저도) 복잡하게 만들기 때문입니다.
소자 기술자들은 적당한 γ 값을 위해 N_sub와 C_ox를 조절합니다.
