출처: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 8 - Feedback (pg. 282~298)
8. Feedback
8.1. General Considerations
Negative Feedback 구조 및 특성, Feedforward, Feedback, Open-loop gain, Closed-loop gain [Razavi][Ch8]
출처: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second EditionChapter 8 - Feedback (pg. 274~282)8. Feedback8.1. General ConsiderationsOverviewFeedback에는 negative feedback과 positive feedback이 있습니다. Negative feedback은
soobdal.tistory.com
Types of Amplifiers

지금까지는 input과 output이 모두 전압인 amp를 공부했습니다.
이 외에도 input과 output이 각각 전류와 전압, 전압과 전류, 전류와 전류인 amp도 있습니다.

각 amp의 간단한 구현과(Fig. 8.14), gain을 높이거나 output impedance를 바꾼 조금 더 복잡한 구현(Fig. 8.15)입니다.
Sense and Return Mechanisms
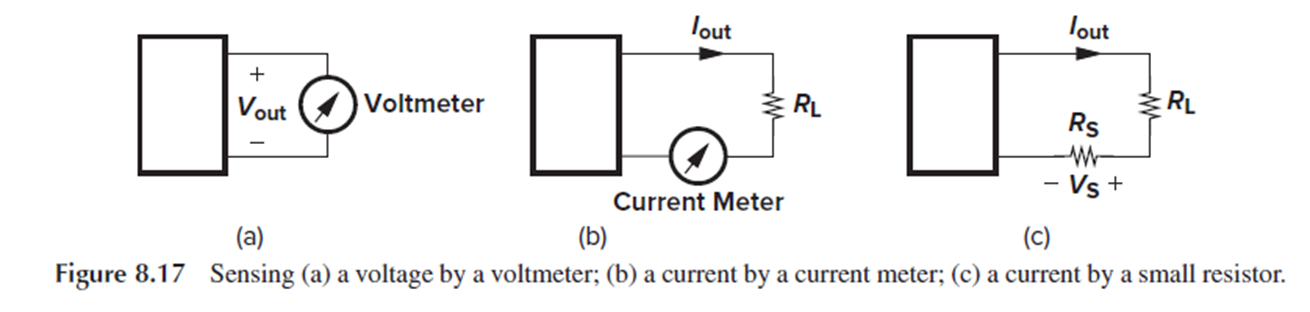
전압을 sensing할 때는 voltmeter를 해당 port에 병렬로 연결합니다.
이것이 feedback에 쓰일 때, shunt feedback이라고 합니다.
전류를 sensing할 때는 current meter를 신호에 직렬로 연결하고, 이런 sensing 방식을 series feedback이라고 합니다.
실제로는 current meter 대신 작은 resistor를 사용합니다.
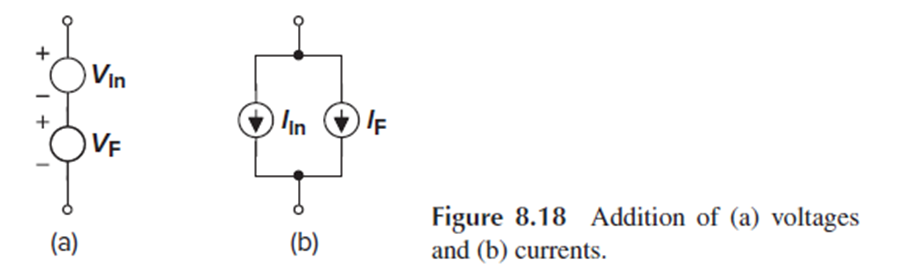
Input signal과 feedback signal을 더할 때, 전압을 더할 때는 두 전압을 직렬로, 두 전류를 더할 때는 병렬로 연결합니다.
즉, feedback이 있는 회로의 input단에서 전압을 더할 때는 직렬, output단에서 전압을 sensing할 때는 병렬연결을 사용하고,
Input단에서 전류를 더할 때는 병렬, output단에서 전류를 sensing할 때는 직렬연결을 사용합니다.
이 내용은 조금 뒤에 쓰일 것입니다.

V 또는 I를 sensing하는 다양한 방법입니다.
(a): Vout에 resistive(또는 capacitive) divider를 병렬로 연결해 Vout sensing
(b), (c): Vf=IoutR1으로 Iout sensing
(d): Differential pair를 사용하여 두 전압의 차를 구함
(e), (f): Id1이 Vin-Vf에 대한 함수이므로 Vin-Vf를 구할 수 있음
(g), (h): 전류의 차를 구할 수 있음
Feedback Topologies
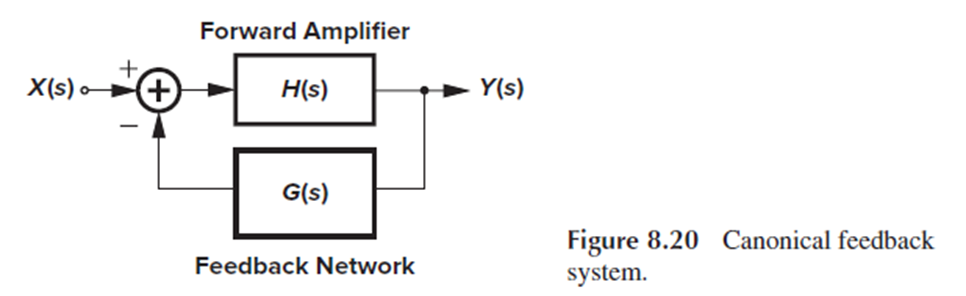
Forward amplifier(feedforward amplifier)에 걸어주는 feedback network로 4개의 amp 종류(V-V, I-V, V-I, I-I) 중에 하나를 사용합니다.
이 4개의 feedback topology를 하나씩 살펴볼 것입니다.
참고로 모든 feedback 회로가 이 4가지에 해당하는 것은 아닙니다.
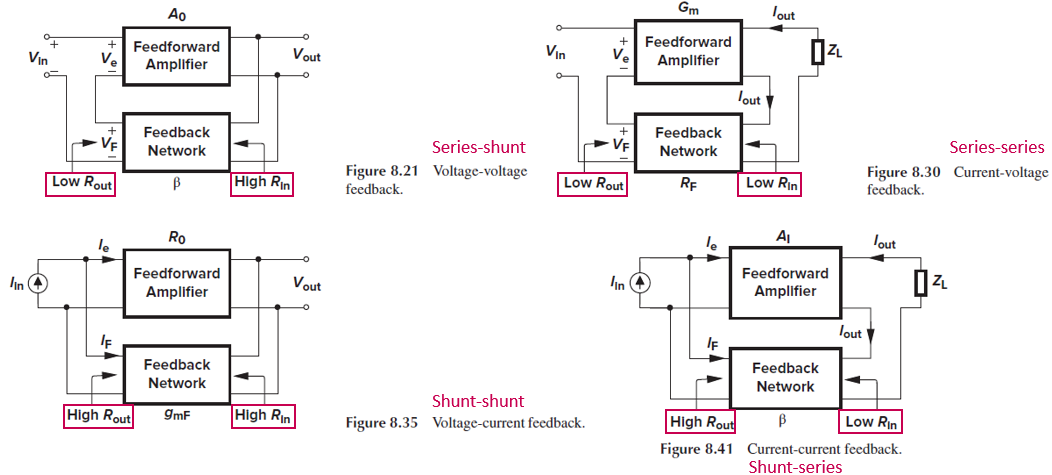
이렇게 네 가지입니다.
- Input단
Negative feedback을 신호를 input에서 뺄 때, 전압 Vf를 Vin에서 뺄 때는 두 전압을 직렬로 연결해서 Ve=Vin-Vf를 만들고,
전류 If를 Iin에서 뺄 때는 두 전류를 병렬로 연결해서 Ie=Iin-If를 만듭니다.
- Output단
전압을 sensing할 때는 신호를 feedback network와 병렬로 연결하는 shunt feedback을 사용하고,
전류를 sensing할 때는 신호와 feedback network를 직렬로 연결하는 series feedback을 사용합니다.
종합해 보면, 4개의 amp가 아래와 같은 이름으로 불리기도 합니다.
왼쪽 명명법에서는 feedforward amp의 output 단을 먼저 읽고, 오른쪽 명명법에서는 feedforward amp의 input 단을 먼저 읽는다는 점을 주의해야 합니다.
- Voltage-voltage feedback == Series-shunt feedback
- Current-voltage feedback == Series-series feedback
- Voltage-current feedback == Shunt-shunt feedback
- Current-current feedback == Shunt-series feedback
1. Voltage-Voltage Feedback (Series-Shunt Feedback)
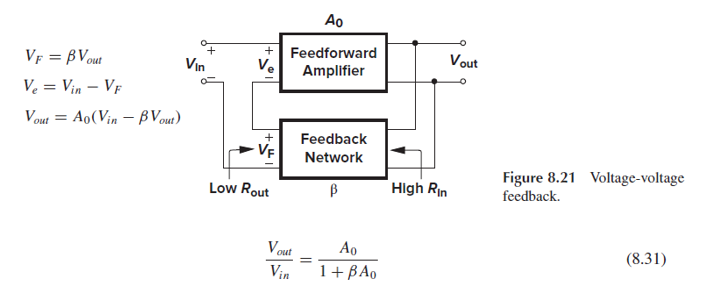
Feedback network가 output과 병렬(V, Shunt), input과 직렬(V, series)로 연결되어 있습니다.
βA0가 loop gain이고, feedback으로 전체 gain이 1+βA0만큼 감소했습니다.
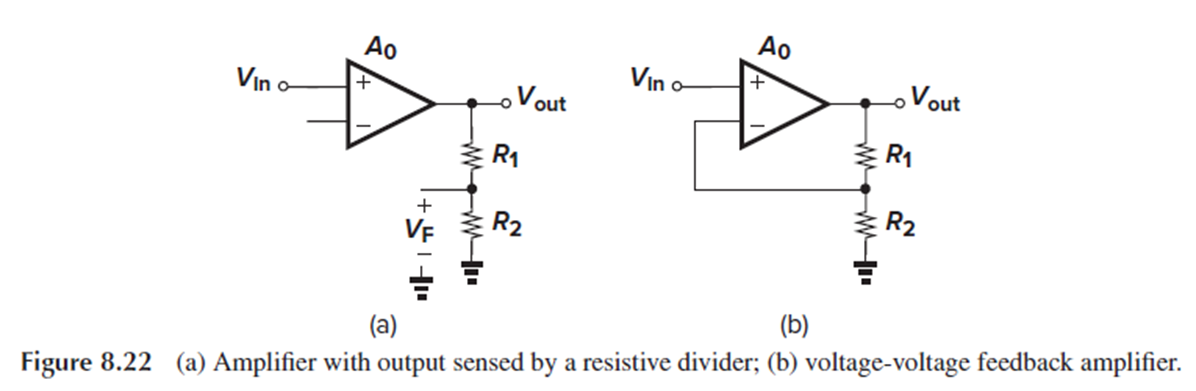
Figure 8.22는 series-shunt feedback의 간단한 예시입니다.
(a): Voltage divider가 output 전압을 sensing해서 feedback signal Vf의 일부를(R2/(R1+R2)배) 따옵니다.
(b): Vf를 Vin과 series로 연결해서 둘의 차를 Amp의 input으로 인가합니다.

Voltage-voltage feedback은 output impedance를 낮추는 특성이 있습니다.
Feedback이 없는 open-loop configuration에서는 Vout이 A0Ve*RL/(RL+Rout)이지만, feedback이 있을 때는 Vout/Vin이 1/β입니다.
Load resistance RL에 관계없이 Vout/Vin이 1/β로 유지된다는 것은, output impedance가 낮다는 것과 같습니다.
*이때 β는 단위가 없는 상수입니다.
Voltage-voltage feedback으로 인해 회로가 voltage source처럼 동작하는 것을 볼 수 있습니다.
* 이러한 특성은 feedback에 의한 gain desensitization에서 기인합니다.

V-V feedback이 output impedance를 감소시킨다는 것을 수식으로 증명해 보겠습니다.
Output impedance와 gain이 같은 비율만큼 감소하는 것을 볼 수 있습니다.
Fig. 8.22(b)에서도, output impedance가 1+A0R2/(R1+R2)만큼 감소했습니다.

Feedback이 없을 때는 feedforward amp의 input impedance가 Vin에 온전히 가해지지만, feedback이 있을 때는 Ve=Vin-Vf에 가해집니다.
따라서 feedback이 있을 때 Rin에 걸리는 전류가 open-loop system에서보다 작습니다.
Feedback이 가해지면 input impedance가 커지는 효과가 나타난다는 것이죠.
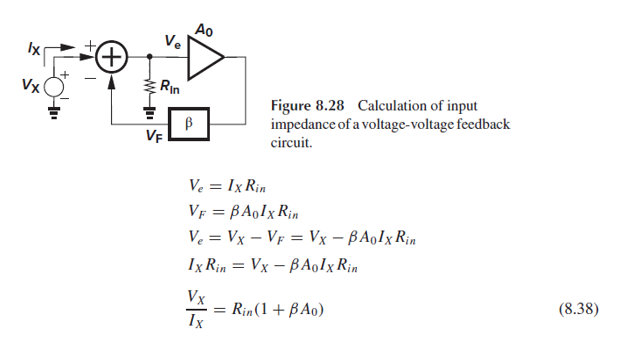
수식으로 증명해 보면, Input impedance는 feedback에 의해 1+βA0만큼 증가하여, 회로가 ideal voltage amp에 가깝게 되는 것을 확인할 수 있습니다.
2. Current-Voltage Feedback (Series-Series Feedback)
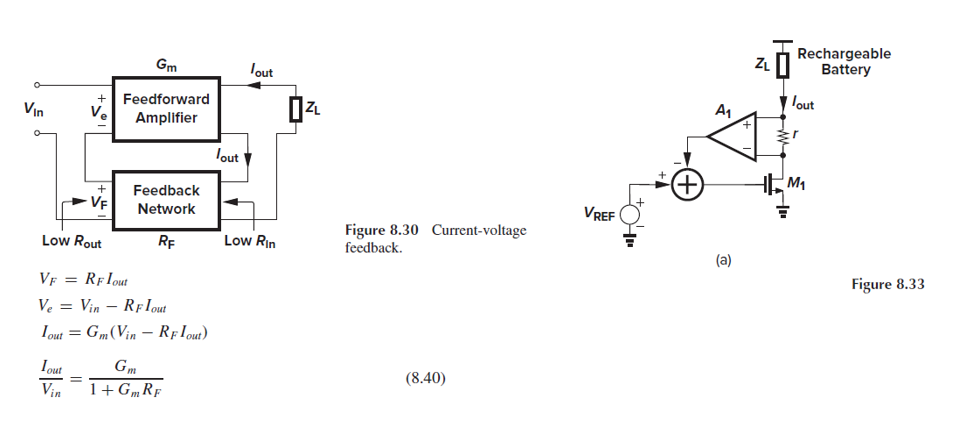
Feedback의 input으로 전류 정보를 받아올 때는 current-voltage feedback, 또는 series-series feedback을 연결합니다.
전류를 sensing하기 위해 output 단이 feedback network와 직렬로 연결되어 있습니다.
Figure. 8.33(a)은 current-voltage feedback의 예시입니다.
A1이 feedback network이고, Iout을 sensing해서 voltage를 생성하고 Vref에서 빼고 있습니다.
*이때 β는 신호가 I에서 V가 되도록 하므로, 저항의 단위를 가지며 Rf로 표현되었습니다.
그리고 Gm stage의 부하가 ZI가 유한한 임피던스여야 Iout이 흐를 수 있습니다.
만약 Zl=∞이면 이상적인 Gm의 경우 Vout=∞라서 Iout이 특정되지 않겠죠.
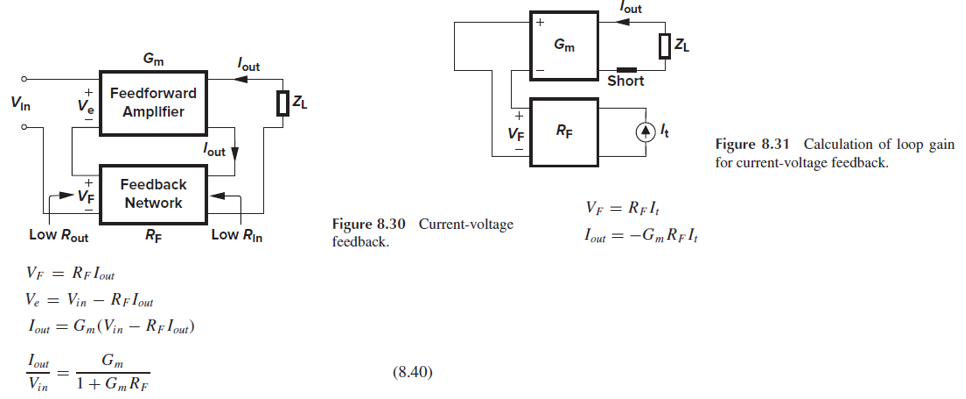
이 구조에서 Iout/Vin = Gm/(1+GmRf)로 나타납니다.
Feedback으로 인해 Gm이 1/(1+GmRf)배 되는 것입니다.
이전에는 보통 Vout/Vin 수식의 GmRf 자리에 loop gain이 있었는데, GmRf도 이 회로의 loop gain입니다.
이를 증명해 보겠습니다.
Loop gain을 계산하기 위해 Fig. 8.31처럼 Vin을 0으로 두고, output 쪽에서 feedback network를 끊고 short시켰습니다.
그런 다음에 test signal It를 인가해 Vf=RfIt를 생성합니다.
그러면 Iout = -GmVf = -GmRfIt, Iout/It = -GmRf로, loop gain이 GmRf임을 알 수 있습니다.
Feedback으로 인해 Gm이 1+(loop gain)만큼 감소한 것입니다.
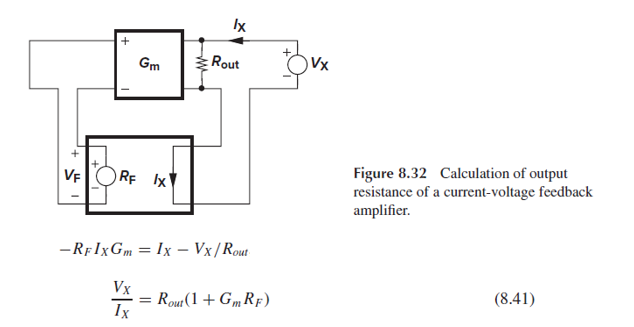
Current-voltage feedback은 output과 input resistance를 둘다 증가시킵니다.
Output resistance를 증가시키는 것부터 증명하겠습니다.
Current-voltage feedback의 feedforward amp의 output impedance를 Rout이라고 둡시다.
((?) 여기서 Rout이 output와 병렬로 연결된 이유는, ideal한 transimpedance amp가 voltage-dependent current source로 모델링되기 때문입니다. )
Feedback network는 Vf=RfIx를 생성하고, 이 전압이 Gm을 거쳐 전류 –RfIxGm을 생성할 것입니다.
이 전류가 Ix-Vx/Rout과 같다고 두고 식을 전개하면, 전체 회로의 output impedance는 (8.41)이 됩니다.
Output impedance가 feedforward amp의 output impedance 대비 (1+GmRf), 즉, (1+loop gain)만큼 증가했습니다.
Ch9에 나오겠지만, 높은 output impedance는 high-gain op amp에 유용하게 사용된다고 합니다.
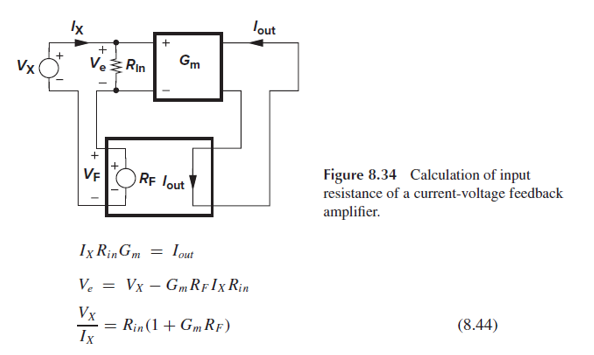
Current-voltage feedback의 input resistance가 증가하는 이유도 살펴보겠습니다.
IxRinGm = Iout이고,
Ve = Vx-Rf*Iout = Vx-Gm*Rf*Ix*Rin이므로,
input resistance Vx/Ix는 Rin(1+GmRf)로 feedforward amp의 Rin 대비 (1+GmRf), 즉, (1+loop gain)만큼 커짐을 증명했습니다.
3. Voltage-Current Feedback (Shunt-Shunt Feedback)

다음은 voltage-current feedback, 또는 shunt-shunt feedback입니다.
직전 경우와 반대로, 전압을 sensing해서 전류를 생성합니다.
이상적인 voltage-current feedback은 input과 output impedance가 모두 ∞입니다.
여기서 feedforward amp는 transimpedance(Vout/Iin) amp로, gain은 Ro입니다.
Feedback factor β는 conductance의 단위를 갖고, gmf라고 명명했습니다.
Fig. 8.36(a)가 voltage-current feedback의 예시입니다.

Voltage-current feedback은 feedforward amp의 transimpedance Ro를 (1+gmfRo)만큼 낮춥니다.
전 case들과 마찬가지로 gmfRo가 loop gain이라서, Ro가 (1+loop gain)만큼 낮아지는 것입니다.

Voltage-current feedback은 input impedance와 output impedance를 둘다 낮추는 특성이 있습니다.
Rin과 Rout은 둘다 port와 직렬로 나타나고, 회로에서 input과 ouput impedance를 구해 보면 두 값이 (1+loop gain)만큼 작아지는 것을 알 수 있습니다.
Input impedance가 작은 amp는 광통신에 쓰이곤 합니다.
광섬유로 들어온 빛이 reverse-biased photodiode에 의해서 전류로 변환되고, 다시 전압으로 변환되어 회로에서 사용됩니다.
4. Current-Current Feedback(Shunt-Series Feedback)

마지막은 current-current feedback, 다른 말로는 shunt-series feedback입니다.
Input과 output이 모두 전류이므로 feedforward amp의 current gain Ai와 feedback factor β에는 단위가 없습니다.
Closed-loop current gain은 (1+βAi)배 감소하고, input impedance도 (1+βAi)배 감소하고, output impedance는 (1+βAi)배 증가하는 특성을 띱니다.
Fig. 8.42가 voltage-current feedback의 예시입니다.
Review: Feedback Topologies
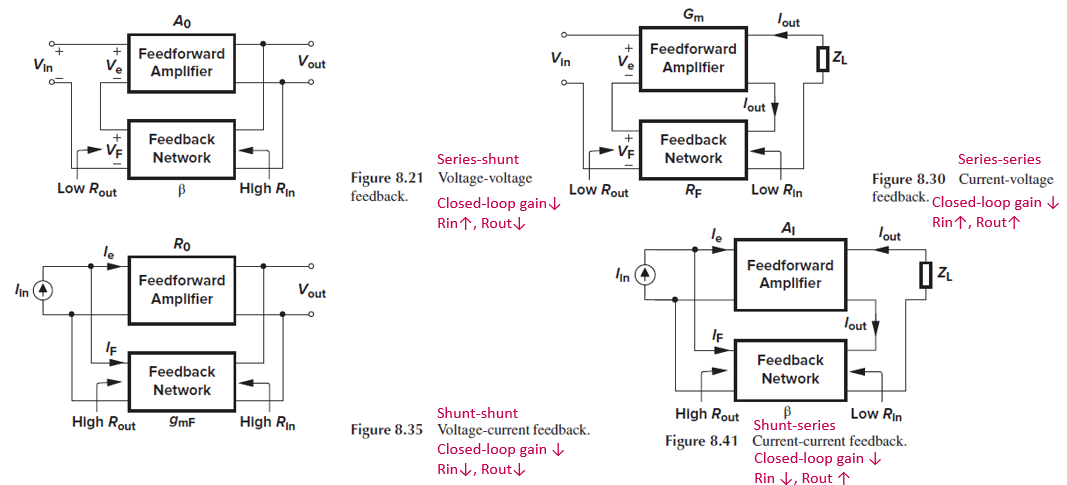
지금까지 알아본 4가지 feedback topology를 정리한 것입니다.
모든 topology에서 closed-loop gain은 공통적으로 (1+loop gain)만큼 감소해서, gain이 feedforward gain 변화에 덜 민감하게 됩니다.
Shunt면 impedance가 감소하고, series면 impedance가 증가하는 특성이 있습니다.
'CMOS IC Design' 카테고리의 다른 글
| Negative Feedback 구조 및 특성, Feedforward, Feedback, Open-loop gain, Closed-loop gain [Razavi][Ch8] (0) | 2025.01.16 |
|---|---|
| Miller Effect의 정의, 의의 및 한계, Gain-Bandwidth Product(GBW) [Razavi][Ch6] (0) | 2025.01.08 |
| Circuit Biasing Techniques [Razavi][Ch5] (0) | 2025.01.08 |
| Active Current Mirrors [Razavi][Ch5] (0) | 2025.01.07 |
| Differential pair with MOS Loads, Gilbert Cell [Razavi][Ch4] (0) | 2025.01.07 |



