참고: Behzad Razavi, Design of Analog CMOS Integrated Circuits, Second Edition
Chapter 2 - Basic MOS Device Physics (pg.27~31)
2.4. MOS Device Models
2.4.2. MOS Device Capacitances
5개의 MOSFET Device Capacitance(Parasitic Capacitance)
이전 section에서 살펴본 MOSFET의 I/V 관계(body effect, channel-length modulation 등을 포함한)는 CMOS 회로의 low-frequency behavior에 대한 것입니다.
하지만, 아날로그 회로에서 high-frequency behavior까지 예측하기 위해서는, MOSFET의 여러 capacitance까지 고려해야 합니다.

MOSFET의 4개 terminal(G, S, D, B) 중 모든 2개 terminal의 연결에는 capacitance가 존재합니다. (Figure 2.31)
경우의 수 4C2 = 6인데, S와 D 사이의 capacitance는 무시 가능하여 5개의 capacitance(Cgd, Cgs, Cdb, Csb, Cgb)가 있습니다.
나아가, 각 capacitance의 값은 transistor의 bias condition에 의존합니다.

Figure 2.32(a)의 구조에서, 아래의 capacitance가 생깁니다.
(1) Gate와 channel 사이의 oxide capacitance, C1 = W * L * C_ox
(2) Channel과 substrate 사이의 depletion capacitance, C2

C1와 C2를 직렬 연결한 값이 Cgb와 같을 것입니다.
(3) Gate poly가 source와 drain area와 overlap되어 생기는 overlap capacitance, C3(Cgs)와 C4(Cgd)
단위 width 당 overlap capacitance를 Cov라고 하며, 단위는 [F/m](또는 [fF/μm])입니다.
C3과 C4의 값은, 즉 Cgs와 Cgd의 값은 Cov * W입니다.
(4) Source/drain area와 substrate 사이의 junction capacitance (Csb, Cdb)
Figure 2.32(b)에서 보듯, 이 capacitance는 두 개의 component로 구성되어 있습니다.
① Cj: junction의 아랫면과 관련이 있는 bottom-plate capacitance [F/m^2]
② Cjsw: junction의 옆면, 즉 둘레(perimeter value)와 관련이 있는 sidewall capacitance [F/m]
이렇게 두 개의 component를 구분하는 이유는, transistor의 geometry에 따라 S/D junction의 면적과 둘레가 다르기 때문입니다.
Cj의 단위는 [F/m^2], Cjsw의 단위는 [F/m]이기 때문에 Cj는 S/D 면적으로 곱해지고, Cjsw는 S/D의 둘레로 곱해집니다.

예를 들어, Figure 2.33(a)의 junction capacitance가 아래와 같이 나타나고,

Figure 2.33(b)의 "folded" structure에서 junction capacitance는 아래와 같습니다.

Figure 2.33(b)의 folded structure는 Figure 2.33(a)과 같은 W/L를 가지면서 drain junction capacitance가 훨씬 더 작습니다.
MOSFET이 OFF일 때의 Capacitance
이제 MOSFET이 동작하는 region(off, triode region, saturation region)별로 terminal간 capacitance를 구해보겠습니다.

먼저 device가 off일 때, Cgd = Cgs = Cov*W이고, gate-bulk capacitance는 gate-oxide capacitance와 depletion-region capacitance의 series combination입니다. (Figure 2.32(a))
이를 수식으로 적으면 다음과 같습니다.
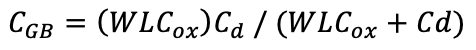
L은 effective length이고, Cd는 아래와 같습니다.
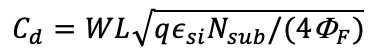
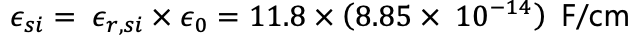
Csb와 Cdb 값은 substrate에 대한 source와 drain voltage의 함수입니다.
Triode Region에서의 MOSFET Capacitance
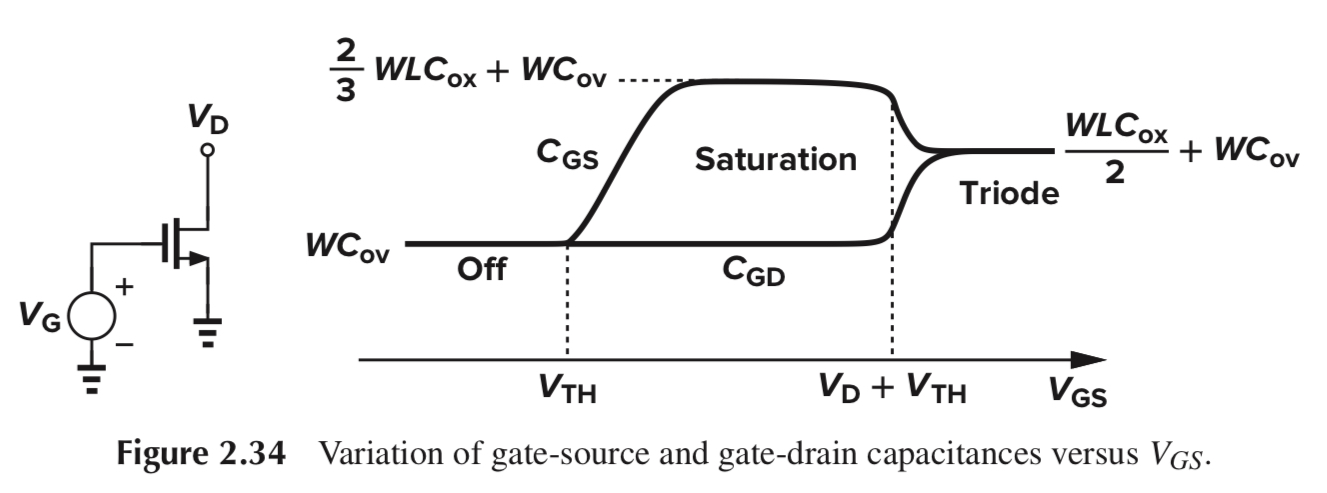
Device가 deep triode region에 있을 때, 즉, S와 D 전압이 거의 같다면 gate-channel capacitance인 W*L*Cox는 gate와 source terminal 사이, gate와 drain terminal 사이에서 똑같이 나눠집니다. (Figure 2.34)(중요한 그래프!!)
Vg가 변할 때, S와 D 전압이 거의 같으니 S와 D로부터 같은 양의 charge가 이동하기 때문입니다.
따라서, Cgd = Cgs = W*L*Cox/2 + W*Cov 입니다.
위에서 살펴본 Cgd = Cgs = W*Cov에, W*L*Cox/2 항을 더한 것이죠.
Saturation Region에서의 MOSFET Capacitance
Saturation에서는 pinch-off에 의해 MOSFET의 drain 근처에 charge carrier가 없을 것입니다.
따라서 Cgd에 gate-channel capacitance W*L*Cox 성분이 더해지지 않고 Cgd ≒ W*Cov가 됩니다.
Cgs의 경우, gate와 channel의 전압차가 source에서 Vgs, pinch-off point에서 Vth가 됩니다.
(Pinch-off는 channel 상에서 전압이 Vgs - Vth인 지점에서 일어나기 때문입니다.)
Gate-channel capacitance의 2/3만큼만, 즉, (2/3)W*Leff*Cox만큼만 Cgs에 더해지게 된다고 합니다.
Cgs = 2*W*Leff*Cox/3 + W*Cov인 것이죠.
Saturation region에서의 Cgd와 Cgs 그래프 역시 Figure 2.34에서 확인할 수 있습니다.
참고로, gate-bulk capacitance Cgb는 triode와 saturation region에서 무시하는 경우가 많습니다.
Inversion layer가 gate와 bulk 사이의 방패(shield) 역할을 하기 때문에, Vg가 변할 때 charge가 bulk보다는 source와 drain에서 이동하기 때문입니다.
'CMOS IC Design' 카테고리의 다른 글
| FinFETs, MOSCAP [Razavi][Ch2] (0) | 2024.10.29 |
|---|---|
| Small-Signal Model [Razavi][Ch2] (1) | 2024.10.07 |
| MOSFET Device Layout(Contact Window, Metal Wire, Design Rule) [Razavi][Ch2] (1) | 2024.10.06 |
| MOSFET Second-Order Effects(4) - Voltage Limatations, Punch-Through [Razavi][Ch2] (1) | 2024.10.06 |
| MOSFET Second-Order Effects(3) - Subthreshold Conduction [Razavi][Ch2] (1) | 2024.10.06 |



